Advertisements (Quảng cáo)
Cho tam giác ABC, trong đó \(BC = 20cm,\widehat {ABC} = {22^o},\widehat {ACB} = {30^o}\).
a) Tính khoảng cách từ điểm B đến đường thẳng AC.
b) Tính khoảng cách từ điểm A đến đường thẳng BC.
c) Tính các cạnh và góc còn lại của tam giác ABC.
Sử dụng các hệ thức về cạnh và góc trong tam giác vuông và định lý tổng 3 góc trong tam giác để tính.
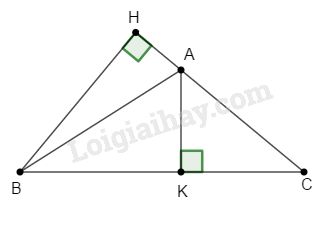
a) Tính khoảng cách từ điểm B đến đường thẳng AC.
Gọi khoảng cách từ điểm B đến đường thẳng AC là BH
Xét tam giác BHC vuông tại H: \(BH = BC.\sin \widehat {ACB} = 20.\sin {30^o} = 10\,\,(cm)\)
Advertisements (Quảng cáo)
b) Tính khoảng cách từ điểm A đến đường thẳng BC.
Xét tam giác BHC vuông tại H \( \Rightarrow \widehat {HBC} = {90^o} – \widehat {ACB} = {60^o}\)
\( \Rightarrow \widehat {HBA} = \widehat {HBC} – \widehat {ABC} = {60^o} – {22^o} = {38^o}\)
Xét tam giác BHA vuông tại H: \(BH = BA.\cos \widehat {HBA}\)
\(\Rightarrow BA = \dfrac{{BH}}{{\cos \widehat {HBA}}} = \dfrac{{10}}{{\cos {{38}^o}}}\,\,(cm)\)
Gọi khoảng cách từ điểm A đến đường thẳng BC là AK
Xét tam giácAKB vuông tại K: \(AK = BA.\sin \widehat {ABC}\)\(\, = \dfrac{{10}}{{\cos {{38}^o}}}.\sin {22^o} \approx 4,75\,\,(cm)\)
c) Tính các cạnh và góc còn lại của tam giác ABC.
Xét tam giácAKC vuông tại K: \(AK = AC.\sin \widehat {ACB} \) \(\Rightarrow AC = \dfrac{{AK}}{{\sin \widehat {ACB}}} \approx 9,51\,\,(cm)\)
Xét tam giác ABC có:
\(\widehat {BAC} = {180^o} – \widehat {ABC} – \widehat {ACB}\)\(\, = {180^o} – {22^o} – {30^o} = {128^o}\)(định lý tổng 3 góc trong tam giác)