Bài 11. Từ một điểm \(P\) ở ngoài đường tròn \((O)\), kẻ cát tuyến \(PAB\) và \(PCD\) tới đường tròn. Gọi \(Q\) là một điểm nằm trên cung nhỏ \(BD\) (không chứa \(A\) và \(C\)) sao cho \(sđ\overparen{BQ}=42^0\) và \(sđ\overparen{QD}=38^0\). Tính tổng \(\widehat {BP{\rm{D}}} + \widehat {AQC}\)
Hướng dẫn làm bài:
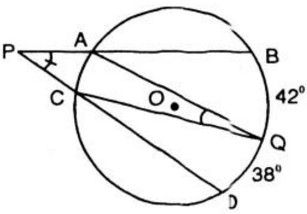
Ta có \(\widehat {BP{\rm{D}}}\) là góc ở ngoài đường tròn (O) nên:
\(\widehat {BPD} = {sđ\overparen{BQD} -sđ\overparen{AC}\over 2}\)
Ta có \(\widehat {AQC}\) là góc nội tiếp trong đường tròn (O) nên:
Advertisements (Quảng cáo)
\(\widehat {AQC} = {1 \over 2}sđ\overparen{AC}\)
Do đó:
\(\widehat {BPD} + \widehat {AQC} = {sđ\overparen{BQD} -sđ\overparen{AC} \over 2} + {1 \over 2}sđ\overparen{AC}\)
=\({1 \over 2}sđ\overparen{BQD}\)=\({{{{42}^0} + {{38}^0}} \over 2} = {40^0}\)
Vậy \(\widehat {BP{\rm{D}}} + \widehat {AQC} = {40^0}\)
