Cho tam giác ABC vuông tại A, hãy tính các tỷ số lượng giác của góc C. Bài 15 trang 77 sgk Toán 9 - tập 1 - Bài 2. Tỉ số lượng giác của góc nhọn
Cho tam giác ABC vuông tại A. Biết cos B=0,8, hãy tính các tỷ số lượng giác của góc C.
Gợi ý: Sử dụng bài tập 14.
Hướng dẫn giải:
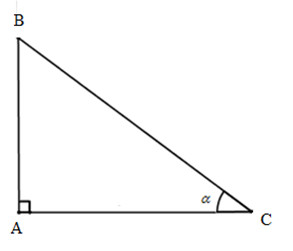
Vì tam giác ABC vuông tại A nên góc C nhọn. Vì thế:
\(sinC>0;\,\,\,cosC>0;\,\,\,tanC>0;\,\,\,cotC>0\)
Vì hai góc B và C phụ nhau nên sinC = cosB = 0,8.
Advertisements (Quảng cáo)
Ta có:
\(Sin^{2}C+cos^{2}C=1\)
\(\Rightarrow cos^{2}C=1-sin^{2}C=1-(0,8)^{2}=0,36\)
\(\Rightarrow cosC=0,6;\)
\(tgC=\frac{sinC}{cosC}=\frac{0,8}{0,6}=\frac{4}{3};\)
\(cotgC=\frac{cosC}{sinC}=\frac{0,6}{0,8}=\frac{3}{4}\)
Nhận xét: Nếu biết \(sin\alpha\) (hay \(cos\alpha\)) thì ta có thể tính được ba tỷ số lượng giác còn lại.