Bài 31. Cho đường tròn (O; R). Bài 31 trang 79 sgk Toán lớp 9 tập 2 - Bài 4. Góc tạo bởi tia tiếp tuyến và dây cung
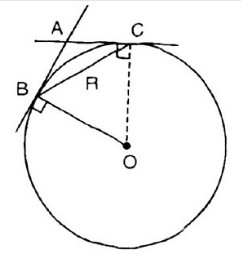
Bài 31. Cho đường tròn \((O; R)\) và dây cung \(BC = R\). Hai tiếp tuyến của đường tròn \((O)\) tại \(B, C\) cắt nhau tại \(A\). Tính \(\widehat {ABC},\widehat {BAC}\).
Hướng dẫn giải:
Advertisements (Quảng cáo)
\(\widehat {ABC}\) là góc tạo bởi hai tiếp tuyến \(BA\) và dây cung \(BC\) của \((O)\). Dây \(BC = R\) suy ra \(\overparen{BC}=60^0\) và \(\widehat {ABC}=30^0\).
\(\widehat {BAC} = {180^0} - \widehat {BOC} = {180^0} - {60^0} = {120^0}\) (tổng các góc của một tứ giác bằng \(360^0\)).
