Tam giác ABC vuông tại C có AC = 15cm. Đường cao CH chia AB thành hai đoạn AH và HB. Biết HB = 16cm. Tính diện tích tam giác ABC.. Bài 5 trang 134 SGK Toán 9 tập 2 - Phần Hình học - Ôn tập cuối năm - Toán 9
Bài 5. Tam giác \(ABC\) vuông tại \(C\) có \(AC = 15cm\). Đường cao \(CH\) chia \(AB\) thành hai đoạn \(AH\) và \(HB\). Biết \(HB = 16cm\). Tính diện tích tam giác \(ABC\).
Hướng dẫn làm bài:
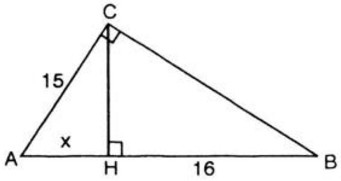
Đặ \(AH = x\) (\(x > 0\))
Áp dụng hệ thức lượng trong tam giác vuông \(ABC\), ta có: \(AC^2 = AB.AH\)
hay \(15^2 = (x + 16)x\) ⇔ \(x^2+ 16x -225 = 0\)
Advertisements (Quảng cáo)
Giải phương trình, ta được \(x_1 = 9\) (thỏa mãn); \(x_2 = -25\) (loại)
Vậy \(AH = 9\) (\(cm\))
Ta có: \(HC^2 = AH. HB = 9. 16 = 144\)
\(\Rightarrow\)\(HC=12\) (\(cm\))
Vậy diện tích tam giác \(ABC\) là:
\(S = {1 \over 2}AB.CH = {1 \over 2}.25.12 = 150(c{m^2})\)