Bài 8. Tìm x và y trong mỗi hình sau:
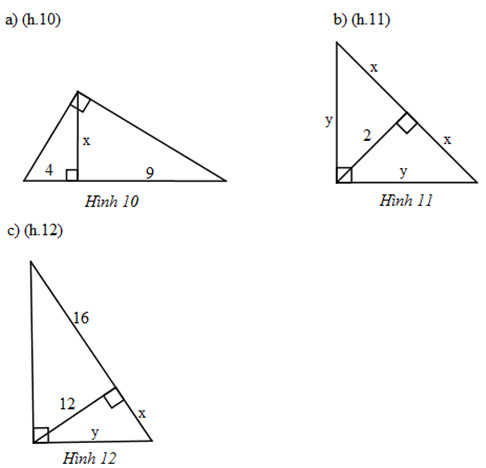
Hướng dẫn giải:
a) Dùng hệ thức lượng bình phương đường cao bằng tích hai hình chiếu hai cạnh góc vuông lên cạnh huyền \(h^{2}=b’c’\)
\(\eqalign{
& \Rightarrow {x^2} = 4.9 = 36 \cr
& \Rightarrow x = 6 \cr} \)
b) Xét tam giác ABC có cạnh huyền là 2x, ta nhận thấy rằng, tam giác này là tam giác vuông cân. Mặc khác, đường cao của tam giác này có độ lớn bằng 2 nên:
\(\frac{1}{y^2}+\frac{1}{y^2}=\frac{1}{2^2}\Rightarrow y=2\sqrt{2}\)
Advertisements (Quảng cáo)
Cạnh huyền của tam giác lớn có độ lớn là 2x, áp dụng định lí Pytago vào tam giác vuông lớn, ta có:
\(2x=\sqrt{y^2+y^2}=\sqrt{8+8}=4\Rightarrow x=2\)
c) Xét tam giác vuông lớn, ta có:
\(12^2=16x\Rightarrow x=9\)
Xét tam giác vuông có cạnh huyền là y, ta có:
\(y^2=\sqrt{12^2+9^2}=15\)
