Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề. Trong tam giác vuông. Trả lời - Bài 3 trang 79 vở thực hành Toán 9 - Bài 12. Một số hệ thức giữa cạnh - góc trong tam giác vuông và ứng dụng. Tính góc nghiêng (alpha ) và chiều rộng AB của mái nhà kho trong Hình 4.16 (góc làm tròn đến độ, độ dài làm tròn đến dm)...

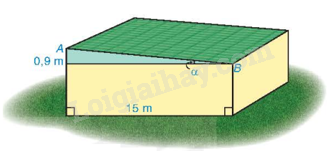
Tính góc nghiêng \(\alpha \) và chiều rộng AB của mái nhà kho trong Hình 4.16 (góc làm tròn đến độ, độ dài làm tròn đến dm).

Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Advertisements (Quảng cáo)
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tan góc đối hoặc nhân với côtang góc kề.

Ta có \(\tan \alpha = \frac{{0,9}}{{15}} = \frac{3}{{50}}\)
Từ đó dùng MTCT suy ra \(\alpha \approx {3^o}\).
Khi đó, \(\sin {3^o} = \frac{{0,9}}{{AB}}\), suy ra \(AB = \frac{{0,9}}{{\sin {3^o}}} \approx 17,2\left( m \right)\).
