
Tính các góc của hình thoi có hai đường chéo dài \(2\sqrt 3 \) và 2.

+ Hình thoi ABCD có \(AC = 2\sqrt 3 ,BD = 2\) nên tính được AO, BO.
+ Tam giác AOB vuông tại O nên \(\tan \widehat {BAO} = \frac{{BO}}{{AO}}\) từ đó tính được góc BAO.
+ Vì ABCD là hình thoi nên \(\widehat {BAD} = 2\widehat {BAO}\), \(\widehat {ABC} = {180^o} - \widehat {BAD}\).

(H.4.17)
Advertisements (Quảng cáo)
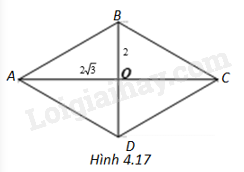
Hình thoi ABCD có \(AC = 2\sqrt 3 ,BD = 2\)
Ta có: \(AO = \frac{1}{2}AC = \sqrt 3 ,BO = \frac{1}{2}BD = \frac{1}{2}.2 = 1\)
Dễ thấy tam giác ABO vuông tại O.
Trong tam giác vuông ABO có \(\tan \widehat {BAO} = \frac{{BO}}{{AO}} = \frac{1}{{\sqrt 3 }}\), suy ra \(\widehat {BAO} = {30^o}\), do đó \(\widehat {BAD} = 2\widehat {BAO} = {2.30^o} = {60^o}\)
Do ABCD là hình thoi nên \(\widehat {ABC} = {180^o} - \widehat {BAD} = {180^o} - {60^o} = {120^o}\)
Vậy hình thoi ABCD có một góc bằng 60 độ và góc kia bằng 120 độ.
