
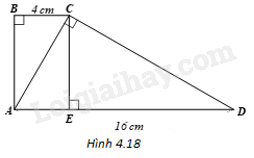
Cho hình thang ABCD (AD//BC) có \(AD = 16cm,BC = 4cm\) và \(\widehat A = \widehat B = \widehat {ACD} = {90^o}\).
a) Kẻ đường cao CE của tam giác ACD. Chứng minh \(\widehat {ADC} = \widehat {ACE}\). Tính sin của các góc \(\widehat {ADC},\widehat {ACE}\) và suy ra \(A{C^2} = AD.AE\). Từ đó tính AC.
b) Tính góc D của hình thang.

a) + Ta có: \(\widehat {ADC} + \widehat {CAD} = {90^o}\), \(\widehat {ACE} + \widehat {CAD} = {90^o}\) suy ra \(\widehat {ADC} = \widehat {ACE}\)
+ Tính được: \(\sin \widehat {ADC} = \frac{{AC}}{{AD}}\), \(\sin \widehat {ACE} = \frac{{AE}}{{AC}}\). Suy ra \(\frac{{AC}}{{AD}} = \frac{{AE}}{{AC}}\), suy ra \(A{C^2} = AD.AE\), tính được AC.
b) Trong tam giác ACD, ta có \(\sin D = \frac{{AC}}{{AD}}\) nên tính được góc D.
Advertisements (Quảng cáo)

(H.4.18)
a) Ta có: \(\widehat {ADC} + \widehat {CAD} = {90^o}\), \(\widehat {ACE} + \widehat {CAD} = {90^o}\) suy ra \(\widehat {ADC} = \widehat {ACE}\)
Trong tam giác ACD, ta có \(\sin \widehat {ADC} = \frac{{AC}}{{AD}}\).
Trong tam giác ACE, ta có \(\sin \widehat {ACE} = \frac{{AE}}{{AC}}\).
Suy ra \(\frac{{AC}}{{AD}} = \frac{{AE}}{{AC}}\), suy ra \(A{C^2} = AD.AE = 64\), từ đó \(AC = 8\)
b) Trong tam giác ACD, ta có \(\sin D = \frac{{AC}}{{AD}} = \frac{8}{{16}} = \frac{1}{2}\) nên \(\widehat D = {30^o}\).
