
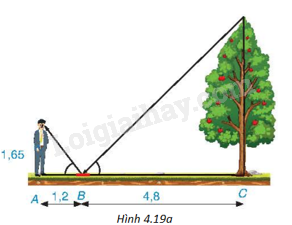
Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2m, nhìn thấy hình phản chiếu qua gương B của ngọn cây (cây mọc thẳng đứng, có gốc ở tại điểm C cách B là 4,8m, B nằm giữa A và C). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65m. Tính chiều cao của cây (H.4.19a).

+ Gọi A’ là điểm tại mắt người đứng, C’ là đỉnh ngọn cây (H.4.19b) thì theo quang học, ta có \(\widehat {ABA’} = \widehat {CBC’}\). Khi đó,
+ Vì \(\tan \widehat {ABA’} = \frac{{AA’}}{{AB}} = \frac{{1,65}}{{1,2}}\), \(\tan \widehat {CBC’} = \frac{{CC’}}{{CB}}\) nên \(\frac{{CC’}}{{BC}} = \frac{{1,65}}{{1,2}}\), từ đó tính được CC’.

Advertisements (Quảng cáo)
Gọi A’ là điểm tại mắt người đứng, C’ là đỉnh ngọn cây (H.4.19b) thì theo quang học, ta có \(\widehat {ABA’} = \widehat {CBC’}\).
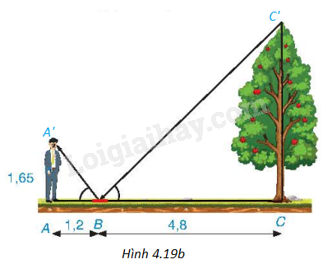
Trong tam giác ABA’, ta có \(\tan \widehat {ABA’} = \frac{{AA’}}{{AB}} = \frac{{1,65}}{{1,2}}\);
Trong tam giác CBC’, ta có \(\tan \widehat {CBC’} = \frac{{CC’}}{{CB}}\).
Vì nên hay \(\frac{{CC’}}{{BC}} = \frac{{1,65}}{{1,2}}\)
Suy ra \(CC’ = \frac{{1,65BC}}{{1,2}} = \frac{{1,65.4,8}}{{1,2}} = 6,6\left( m \right)\).
