
Một người đứng cách gốc cây 20m nhìn thấy ngọn cây với góc \({36^o}\) so với phương nằm ngang. Biết mắt người ấy cách mặt đất 1,7m và cây mọc thẳng đứng (H.4.21a). Tính chiều cao của cây (làm tròn đến chữ số thập phân thứ nhất).
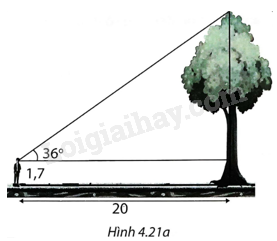

+ Gọi điểm mắt người nhìn là A, ngọn cây là O, gốc cây là H, giao điểm của đường thẳng qua A song song với mặt đất là B. Ta cần tính đoạn OH.
+ Tam giác ABO vuông tại B nên \(OB = AB.\tan \widehat {BAO}\) nên tính được OB.
+ \(OH = BH + OB\), với \(BH = 1,7m\).

Advertisements (Quảng cáo)
(H.4.21b)
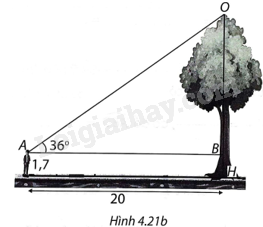
Gọi điểm mắt người nhìn là A, ngọn cây là O, gốc cây là H, giao điểm của đường thẳng qua A song song với mặt đất là B. Ta cần tính đoạn OH.
Ta có \(AB = 20m\) và tam giác ABO vuông tại B.
Trong tam giác vuông ABO có
\(OB = AB.\tan \widehat {BAO} = 20.\tan {36^o} = 20.\sqrt {5 - 2\sqrt 5 } \approx 14,5\left( m \right)\)
Ta có: \(OH = OB + BH \approx 16,2\left( m \right)\)
Vậy cây cao khoảng 16,2m.
