
Cho tam giác ABC vuông tại A, \(BC = 10,AB = 6\).
a) Giải tam giác ABC.
b) Từ B kẻ đường thẳng vuông góc với BC, cắt AC tại D. Tính BD, CD, AD và góc ABD. (Góc làm tròn đến độ, cạnh làm tròn đến chữ số thập phân thứ nhất).

a) + Áp dụng định lý Pythagore vào tam giác ABC vuông tại A tính được AC.
+ \(\sin C = \frac{{AB}}{{CB}}\) từ đó tính góc C, \(\widehat B = {90^o} - \widehat C\) tính được góc B.
b) + Tam giác BCD vuông tại B, ta có: \(\tan C = \frac{{BD}}{{CB}}\) nên tính được BD.
+ Áp dụng định lý Pythagore vào tam giác BCD vuông tại B tính được CD.
+ \(AD = CD - AC\) từ đó tính được AD; \(\sin \widehat {ABD} = \frac{{AD}}{{BD}}\) nên tính được góc ABD.

Advertisements (Quảng cáo)
(H.4.22)
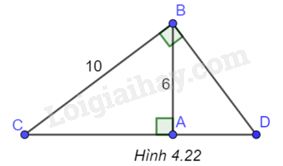
a) Tam giác ABC vuông tại A, theo định lý Pythagore, ta có \(A{C^2} + A{B^2} = B{C^2}\)
\(A{C^2} = B{C^2} - A{B^2} = 64\) nên \(AC = \sqrt {64} = 8\)
\(\sin C = \frac{{AB}}{{CB}} = \frac{3}{5}\) nên \(\widehat C \approx {37^o}\)
Do đó, \(\widehat B = {90^o} - \widehat C = {53^o}\)
b) Tam giác BCD vuông tại B, ta có \(\tan C = \frac{{BD}}{{CB}}\) nên \(BD = BC.\tan C = 10.\tan {37^o} \approx 7,5\)
\(C{D^2} = B{C^2} + B{D^2} = {10^2} + {7,5^2} = \frac{{625}}{4}\).
Do đó, \(CD = \sqrt {\frac{{625}}{4}} = \frac{{25}}{2}\)
Từ đó, \(AD = CD - AC = \frac{{25}}{2} - 8 = \frac{9}{2}\)
Tam giác ABD vuông tại A, ta có \(\sin \widehat {ABD} = \frac{{AD}}{{BD}} = \frac{3}{5}\), do đó, \(\widehat {ABD} \approx {37^o}\)
