Cho hypebol \((H): \dfrac{{{x^2}}}{4} - \dfrac{{{y^2}}}{9} = 1\). Gọi \(\Delta \) là đường thẳng đi qua gốc tọa độ \(O\) và có hệ số góc \(k, \Delta \)’ là đường thẳng đi qua \(O\) và vuông góc với \(\Delta \).
a) Xác định tọa độ các tiêu điểm, tâm sai, phương trình các đường tiệm cận và đường chuẩn của \((H);\)
b) Tìm điều kiện của \(k\) để cả \(\Delta \) và \(\Delta’ \) đều cắt \((H);\)
c) Tứ giác với bốn đỉnh là bốn giao điểm của \(\Delta \) và \(\Delta’ \) với \((H)\) là hình gì ? Tính diện tích của tứ giác này theo \(k ;\)
d) Xác định \(k\) để diện tích tứ giác nói ở câu c) có giá trị nhỏ nhất.

a) \({a^2} = 4 \Rightarrow a = 2 ,\) \({b^2} = 9 \Rightarrow b = 3 , \) \({c^2} = {a^2} + {b^2} = 13 \Rightarrow c = \sqrt {13} \).
Vậy \((H)\) có các tiêu điểm: \({F_1}( - \sqrt {13} ; 0) , {F_2}(\sqrt {13} ; 0)\), tâm sai \(e = \dfrac{c}{a} = \dfrac{{\sqrt {13} }}{2}\), các đường tiệm cận: \(y = \pm \dfrac{{bx}}{a} = \pm \dfrac{3}{2}x\), các đường chuẩn : \(x = \pm \dfrac{a}{e} = \pm \dfrac{4}{{\sqrt {13} }}\).
b) Từ giả thiết suy ra \(\Delta : y = kx, \Delta ‘: y = - \dfrac{1}{k}x\).
Hoành độ giao điểm của \(\Delta \) và \((H)\) là nghiệm của phương trình:
\(9{x^2} - 4{k^2}{x^2} = 36\)
\( \Leftrightarrow (9 - 4{k^2}){x^2} = 36.\) (1)
Tung độ giao điểm của \(\Delta ‘\) và \((H)\) là nghiệm của phương trình:
\(9{k^2}{y^2} - 4{y^2} = 36 \)
\( \Leftrightarrow (9{k^2} - 4){y^2} = 36\). (2)
\(\Delta \) cắt \((H)\) khi và chỉ khi (1) có nghiệm, hay \(9 - 4{k^2} > 0 \Leftrightarrow - \dfrac{3}{2} < k < \dfrac{3}{2}\).
\(\Delta ‘\) cắt \((H)\) khi và chỉ khi (2) có nghiệm, hay \(9{k^2} - 4 > 0 \Leftrightarrow \left[ \begin{array}{l}k > \dfrac{2}{3}\\k < - \dfrac{2}{3}.\end{array} \right.\)
Advertisements (Quảng cáo)
Vậy \(\Delta \) và \(\Delta ‘\) đều cắt \((H)\) khi và chỉ khi \(\left\{ \begin{array}{l} - \dfrac{3}{2} < k < \dfrac{3}{2}\\\left[ \begin{array}{l}k < - \dfrac{2}{3}\\k > \dfrac{2}{3}\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - \dfrac{3}{2} < k < - \dfrac{2}{3}\\ \dfrac{2}{3} < k < \dfrac{3}{2}.\end{array} \right.\)
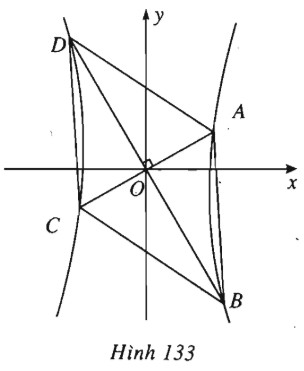
c) Gọi \(A\) và \(C\) là các giao điểm của \(\Delta \) và \((H) (x_A > 0)\); \(B\) và \(D\) là các giao điểm của \(\Delta ‘\) và \((H) (y_B < 0).\)
Do \((H)\) nhận \(O\) làm tâm đối xứng, nên \(OA=OC, OB=OD\), do đó \(ABCD\) là hình bình hành. Lại có \(AC\) vuông góc với \(BD\) nên \(ABCD\) là hình thoi.
Giải hệ các phương trình của \(\Delta \) và \((H)\): \(\left\{ \begin{array}{l} \dfrac{{{x^2}}}{4} - \dfrac{{{y^2}}}{9} = 1\\y = kx\end{array} \right.\), ta được \(A = \left( { \dfrac{6}{{\sqrt {9 - 4{k^2}} }} ; \dfrac{{6k}}{{\sqrt {9 - 4{k^2}} }}} \right)\).
Giải hệ các phương trình của \(\Delta ‘\) và \((H)\) : \(\left\{ \begin{array}{l} \dfrac{{{x^2}}}{4} - \dfrac{{{y^2}}}{9} = 1\\y = - \dfrac{1}{k}x\end{array} \right.\), ta được \(B = \left( { \dfrac{{6k}}{{\sqrt {9{k^2} - 4} }} ; \dfrac{{ - 6}}{{\sqrt {9{k^2} - 4} }}} \right)\).
Ta có :
\(\begin{array}{l}{S_{ABCD}} = 4{S_{OAB}} = 2OA.OB.\\O{A^2} = x_A^2 + y_A^2 = \dfrac{{36({k^2} + 1)}}{{9 - 4{k^2}}} \\ \Rightarrow OA = \dfrac{{6\sqrt {1 + {k^2}} }}{{\sqrt {9 - 4{k^2}} }}\\O{B^2} = x_B^2 + y_B^2 = \dfrac{{36({k^2} + 1)}}{{9{k^2} - 4}} \\ \Rightarrow OB = \dfrac{{6\sqrt {{k^2} + 1} }}{{\sqrt {9{k^2} - 4} }}\\ \Rightarrow {S_{ABCD}} = \dfrac{{72({k^2} + 1)}}{{\sqrt {(9 - 4{k^2})(9{k^2} - 4)} }}\end{array}\).
d) Ta có
\( \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} = \dfrac{{9 - 4{k^2} + 9{k^2} - 4}}{{36(1 + {k^2})}}\)
\(= \dfrac{5}{{36}}\).
Vậy \( \dfrac{1}{{O{A^2}}}. \dfrac{1}{{O{B^2}}}\) lớn nhất \( \Leftrightarrow OA = OB\).
Mà \( \dfrac{1}{{O{A^2}}}. \dfrac{1}{{O{B^2}}}\) lớn nhất \( \Leftrightarrow OA.OB\) nhỏ nhất \({S_{ABCD}}\) nhỏ nhất.
Vậy \(S_ABCD\) nhỏ nhất
\( \Leftrightarrow OA = OB \Leftrightarrow 9 - 4{k^2} = 9{k^2} - 4 \)
\( \Leftrightarrow k = \pm 1\).
Vậy diện tích hình thoi \(ABCD\) nhỏ nhất khi các đường thẳng \(\Delta , \Delta ‘\) là các đường phân giác của góc phần tư thứ nhất và thứ hai.
