Cho elip \((E): \dfrac{{{x^2}}}{4} + \dfrac{{{y^2}}}{1} = 1\) và hai điểm \(M( - 2 ; m), N(2 ; n)\,\,\,\, (m \ne - n)\).
a) Xác định tâm sai, tọa độ các tiêu điểm, các đỉnh và phương trình đường chuẩn của \((E).\)
b) Gọi \(A_1\) và \(A_2\) là các đỉnh trên trục lớn của \((E)\) (\({x_{{A_1}}} < {x_{{A_2}}}\)). Hãy viết phương trình của các đường thẳng \(A_1N\) và \(A_2M\). Xác định tọa độ giao điểm \(I\) của chúng.
c) Biết đường thẳng \(MN\) thay đổi nhưng luôn cắt \((E)\) tại một điểm duy nhất. Tìm tập hợp các giao điểm.
Giải
(h.131).
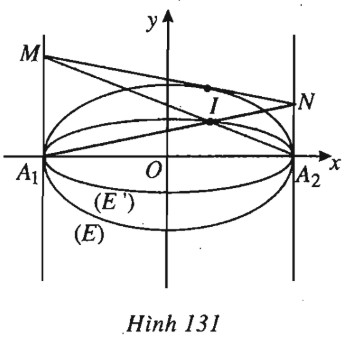
a) \({a^2} = 4 \Rightarrow a = 2 ,\) \( {b^2} = 1 \Rightarrow b = 1 ,\) \( {c^2} = {a^2} - {b^2} = 3 \Rightarrow c = \sqrt 3 \). \((E)\) có:
Các tiêu điểm : \({F_1}( - \sqrt 3 ;0) , {F_2}(\sqrt 3 ; 0)\).
Các đỉnh \({A_1}( - 2 ; 0) , \) \( {A_2}(2 ; 0),\) \( {B_1}(0 ; - 1) ,\) \( {B_2}(0 ; 1)\).
Tâm sai \(e = \dfrac{c}{a} = \dfrac{{\sqrt 3 }}{2}\).
Các đường chuẩn : \(x = \pm \dfrac{a}{e} = \pm \dfrac{4}{{\sqrt 3 }}\).
b) Phương trình đường thẳng \({A_1}N: nx - 4y + 2n = 0\).
Phương trình đường thẳng \({A_2}M: mx + 4y - 2m = 0\).
Advertisements (Quảng cáo)
Tọa độ giao điểm \(I\) là nghiệm của hệ:
\(\left\{ \begin{array}{l}nx - 4y + 2n = 0\\mx + 4y - 2m = 0\end{array} \right. \\ \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{2(m - n)}}{{m + n}}\\y = \dfrac{{mn}}{{m + n}}\end{array} \right.\). Vậy \(I = \left( { \dfrac{{2(m - n)}}{{m + n}} ; \dfrac{{mn}}{{m + n}}} \right)\).
c) Phương trình đường thẳng \(MN:\) \((n - m)x - 4y + 2(m + n) = 0\).
\(MN\) cắt \((E)\) tại một điểm duy nhất khi và chỉ khi hệ \(\left\{ \begin{array}{l}(n - m)x - 4y + 2(m + n) = 0\,\,\,(1)\\ \dfrac{{{x^2}}}{4} + {y^2} = 1\,\,\,\,\,\,\,\,(2)\end{array} \right.\) có đúng một nghiệm.
\((1) \Rightarrow y = \dfrac{1}{4}[(n - m)x + 2(m + n)]\), thay \(y\) vào (2), ta được:
\(\begin{array}{l}{x^2} + 4. \dfrac{1}{{16}}{[(n - m)x + 2(m + n)]^2} = 4\\ \Leftrightarrow [{(n - m)^2} + 4]{x^2} + 4({n^2} - {m^2})x \\+ 4{(m + n)^2} - 16 = 0\,\,\,\,\,\,(3)\end{array}\)
(3) có một nghiệm khi và chỉ khi \(\Delta ‘ = 0\) hay
\(\begin{array}{l}4{({n^2} - {m^2})^2} - [{(n - m)^2} + 4]\\.[4{(n + m)^2} - 16] = 0\\ \Leftrightarrow mn = 1. \,\,\,\,\,\,\,\,\,(4)\end{array}\)
Suy ra tọa độ của I là \(\left\{ \begin{array}{l}x = \dfrac{{2(m - n)}}{{m + n }}\,\,\,\,\,\,\,\,(5)\\y = \dfrac{{mn}}{{m + n}} = \dfrac{1}{{m + n}}\,\,\,\,\,\,\,(6)\end{array} \right.\)
\(\begin{array}{l}(5) \Rightarrow \dfrac{{{x^2}}}{4} = \dfrac{{{{(m - n)}^2}}}{{{{(m + n)}^2}}}\\ = \dfrac{{{m^2} - 2mn + {n^2}}}{{{{(m + n)}^2}}}\\(6) \Rightarrow 4{y^2} = \dfrac{{4mn}}{{{{(m + n)}^2}}}.\end{array}\)
Do đó \( \dfrac{{{x^2}}}{4} + 4{y^2} = 1\).
Vậy tập hợp các giao điểm \(I\) là elip \((E’)\) có phương trình: \( \dfrac{{{x^2}}}{4} + \dfrac{{{y^2}}}{{ \dfrac{1}{4}}} = 1\).
