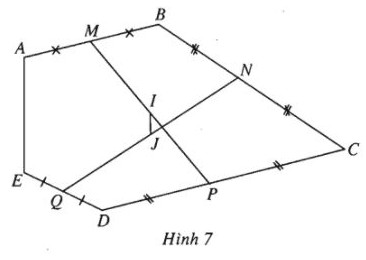
Cho ngũ giác \(ABCDE\). Gọi \(M, N, P, Q\) lần lượt là trung điểm các cạnh \(AB, BC, CD, DE\). Gọi \(I\) và \(J\) lần lượt là trung điểm các đoạn \(MP\) và \(NQ\).
Chứng minh rằng \(IJ// AE\) và \(IJ = \dfrac{1}{4}AE\).

Advertisements (Quảng cáo)
Ta có
\(\eqalign{ & 2\overrightarrow {IJ} = \overrightarrow {IQ} + \overrightarrow {IN} \cr & \,\,\,\,\,\,\,\,\, = \overrightarrow {IM} + \overrightarrow {MQ} + \overrightarrow {IP} + \overrightarrow {PN} \cr & \,\,\,\,\,\,\,\,\, = \overrightarrow {MQ} + \overrightarrow {PN} \cr & \,\,\,\,\,\,\,\,\, = {1 \over 2}(\overrightarrow {AE} + \overrightarrow {BD} ) + {1 \over 2}\overrightarrow {DB} \cr & \,\,\,\,\,\,\,\,\, = {1 \over 2}\overrightarrow {AE} \cr} \)
Vậy \(\overrightarrow {IJ} = \dfrac{1}{4}\overrightarrow {AE} \). Suy ra \(IJ // AE\) và \(IJ = \dfrac{1}{4}AE\).
