Bài 80 trang 116 SBT Hình 10 nâng cao: (1.116)....

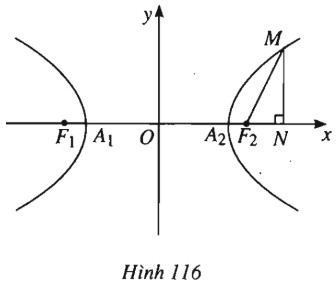
Cho hypebol $(H):  \dfrac{{{x^2}}}{{{a^2}}} -  \dfrac{{{y^2}}}{{{b^2}}} = 1$. Gọi $F_1, F_2$ là các tiêu điểm và $A_1, A_2$ là các đỉnh của $(H)$. $M$ là điểm tùy ý trên $(H)$ có hình chiếu trên $Ox$ là $N$. Chứng minh rằng

a) $O{M^2} - M{F_1}.M{F_2} = {a^2} - {b^2}$;

b) ${(M{F_1} + M{F_2})^2} = 4(O{M^2} + {b^2})$;

c) $N{M^2} =  \dfrac{{{b^2}}}{{{a^2}}}.\overline {N{A_1}} .\overline {N{A_2}}$.

(1.116).

$M(x ; y)  \in (H)   \Leftrightarrow    \dfrac{{{x^2}}}{{{a^2}}} -  \dfrac{{{y^2}}}{{{b^2}}} = 1,$

$M{F_1} = \left| {a +  \dfrac{c}{a}x} \right|  ,  M{F_2} = \left| {a -  \dfrac{c}{a}x} \right|.$

a)Ta có

$\begin{array}{l}O{M^2} - M{F_1}.M{F_2}\\ = {x^2} + {y^2} - \left| {{a^2} -  \dfrac{{{c^2}}}{{{a^2}}}{x^2}} \right|\\ = {x^2} + {y^2} - \left| {{a^2} - {c^2}\left( {1 +  \dfrac{{{y^2}}}{{{b^2}}}} \right)} \right|\\ = {x^2} + {y^2} - \left| { - {b^2} -  \dfrac{{{c^2}}}{{{b^2}}}{y^2}} \right|\\ = {x^2} + {y^2} - {b^2} -  \dfrac{{{c^2}}}{{{b^2}}}{y^2}\\ = {a^2} +  \dfrac{{{a^2}}}{{{b^2}}}{y^2} + {y^2} - {b^2} -  \dfrac{{{a^2} + {b^2}}}{{{b^2}}}{y^2}\\ = {a^2} - {b^2}.\end{array}$

b)

$\begin{array}{l}{(M{F_1} + M{F_2})^2} \\= {(M{F_1} - M{F_2})^2} + 4M{F_1}.M{F_2}\\ = 4{a^2} + 4\left| {{a^2} -  \dfrac{{{c^2}}}{{{a^2}}}{x^2}} \right|\\= 4{a^2} + 4{b^2} +  \dfrac{{4{c^2}}}{{{b^2}}}{y^2} (1)\\4(O{M^2} + {b^2}) = 4({x^2} + {y^2} + {b^2}) \\= 4{x^2} + 4{y^2} + 4{b^2}\\= 4\left( {{a^2} +  \dfrac{{{a^2}}}{{{b^2}}}{y^2}} \right) + 4{y^2} + 4{b^2}\\= 4{a^2} + 4{b^2} + 4{y^2}\left( { \dfrac{{{a^2}}}{{{b^2}}} + 1} \right)\\= 4{a^2} + 4{b^2} +  \dfrac{{4{c^2}}}{{{b^2}}}{y^2}.(2)\end{array}$

Từ (1) và (2) suy ra điều phải chứng minh.

c)

$\begin{array}{l}M{N^2} = {y^2}.\\ \dfrac{{{b^2}}}{{{a^2}}}.\overline {N{A_1}} .\overline {N{A_2}}\\  =  \dfrac{{{b^2}}}{{{a^2}}}( - x - a)( - x + a)\\ =  -  \dfrac{{{b^2}}}{{{a^2}}}({a^2} - {x^2}) =  - {b^2} +  \dfrac{{{b^2}}}{{{a^2}}}{x^2}\\=  - {b^2} + {b^2}\left( {1 +  \dfrac{{{y^2}}}{{{b^2}}}} \right) = {y^2}.\end{array}$

Vậy $N{M^2} =  \dfrac{{{b^2}}}{{{a^2}}}.\overline {N{A_1}} .\overline {N{A_2}}$.