Cho đường tròn \((C)\) có phương trình \({x^2} + {y^2} = 1\). Đường tròn \((C)\) cắt \(Ox\) tại \(A(-1 ; 0)\) và \(B(1 ; 0)\). Đường thẳng \(d\) có phương trình \(x = m ( - 1 < m < 1, m \ne 0)\) cắt \((C)\) tại \(M\) và \(N\). Đường thẳng \(AM\) cắt đường thẳng \(BN\) tại \(K\). Tìm tập hợp các điểm \(K\) khi \(m\) thay đổi.

(h.117).
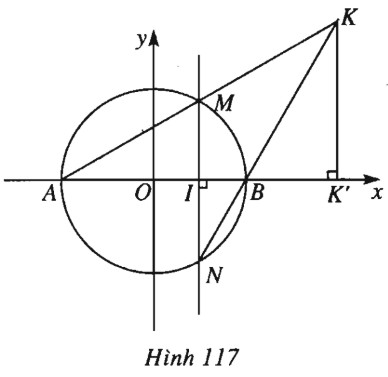
Giả sử \(M = ({x_0} ; {y_0})\), suy ra \(N = ({x_0} ; - {y_0})\). Do \( - 1 < m < 1, m \ne 0\) nên \( - 1 < {x_0}, {y_0} < 1, {x_0} \ne 0, {y_0} \ne 0\). Ta có:
Advertisements (Quảng cáo)
Phương trình đường thẳng \(AM: \dfrac{{x + 1}}{{{x_0} + 1}} = \dfrac{y}{{{y_0}}}\) (1)
Phương trình đường thẳng \(BN: \dfrac{{x - 1}}{{{x_0} - 1}} = \dfrac{y}{{ - {y_0}}}\) (2)
Tọa độ \((x ; y)\) của \(K\) thỏa mãn (1) và (2). Nhân từng vế của (1) và (2) với nhau, ta được : \( \dfrac{{{x^2} - 1}}{{x_0^2 - 1}} = \dfrac{{{y^2}}}{{ - y_0^2}}\). Vì \(M \in (C)\) nên \(x_0^2 + y_0^2 = 1\), suy ra \(x_0^2 - 1 = - y_0^2\). Do đó \({x^2} - 1 = {y^2}\) hay \({x^2} - {y^2} = 1\). Tập hợp các điểm \(K\) là hypebol \( \dfrac{{{x^2}}}{1} - \dfrac{{{y^2}}}{1} = 1\) bỏ đi hai đỉnh : \((-1 ; 0)\) và \((1 ; 0).\)
