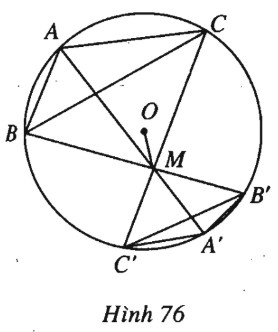
Cho điểm \(M\) nằm trong đường tròn \((O)\) ngoại tiếp tam giác \(ABC\). Kẻ các đường thẳng \(MA, MB, MC,\) chúng cắt lại đường tròn đó lần lượt ở \(A’, B’, C’\). Chứng minh rằng:
\(\dfrac{{{S_{A’B’C’}}}}{{{S_{ABC}}}} = \dfrac{{{{({R^2} - M{O^2})}^3}}}{{{{(MA.MB.MC)}^2}}}\).
Giải
(h.76).
\(\begin{array}{l}{S_{A’B’C’}} = \dfrac{{A’B’.B’C’.C’A’}}{{4R}}.\\{S_{ABC}} = \dfrac{{AB.BC.CA}}{{4R}}.\end{array}\)
Suy ra \(\dfrac{{{S_{A’B’C’}}}}{{{S_{ABC}}}} = \dfrac{{A’B’.B’C’.C’A’}}{{AB.BC.CA}}\) (*)
Advertisements (Quảng cáo)
Ta lại có
\(\Delta MAB \sim \Delta MB’A’\) nên \(\dfrac{{A’B’}}{{AB}} = \dfrac{{MA’}}{{MB}} = \dfrac{{MA.MA’}}{{MA.MB}}\).
Do \(MA.MA’ = |{\wp _{M/(O)}}| = {R^2} - M{O^2}\) nên \(\dfrac{{A’B’}}{{AB}} = \dfrac{{{R^2} - M{O^2}}}{{MA.MB}}\).
Tương tự
\(\dfrac{{B’C’}}{{BC}} = \dfrac{{{R^2} - M{O^2}}}{{MB.MC}} ;\) \( \dfrac{{C’A’}}{{CA}} = \dfrac{{{R^2} - M{O^2}}}{{MC.MA}}\) (**)
Thay (**) vào (*) ta được điều phải chứng minh.
