Cho dây cung \(BC\) của đường tròn \(C(O ; R) (BC<2R).\)
a) Hãy dựng đường tròn tâm \(I\) tiếp xúc với \(OB\) ở \(B\) và tiếp xúc với \(OC\) ở \(C.\)
b) Với mỗi điểm \(M\) trên đường tròn \((I)\), kẻ các đường thẳng \(MB\) và \(MC,\) chúng lần lượt cắt lại đường tròn \((C)\) ở \(B’, C’.\)
Chứng minh rằng \(B’C’\) là đường kính của đường tròn \((C).\)
Giải
(h.77).
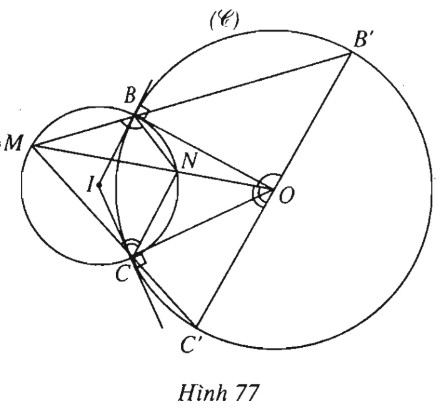
a) Kẻ hai tiếp tuyến của \((C)\) tại \(B\) và \(C\), chúng cắt nhau ở \(I\). Khi đó, dễ thấy đường tròn tâm \(I\) bán kính \(r=IB=IC\) thỏa mãn yêu cầu.
Advertisements (Quảng cáo)
b) Kẻ đường thẳng \(OM,\) nó cắt đường tròn \((I)\) ở \(N\) (\(N \ne M\)), ta có
\(\overrightarrow {OM} .\overrightarrow {ON} = O{B^2}\,\,( = {\wp _{O/(I)}})\).
Từ đó ta có \(\overrightarrow {OM} .\left( {\overrightarrow {OM} + \overrightarrow {MN} } \right) = {R^2}\), suy ra \(O{M^2} - \overrightarrow {OM} .\overrightarrow {MN} = {R^2}\) hay \(\overrightarrow {OM} .\overrightarrow {MN} = O{M^2} - {R^2} \) \(= {\wp _{M/(C)}} = \overrightarrow {MB} .\overrightarrow {MB’} \).
Vậy \(N , B, O, B’\) cùng thuộc một đường tròn, suy ra \(\widehat {NOB’} = \widehat {NBM}\).
Tương tự ta có \(N, C, O, C’\) cùng thuộc một đường tròn, suy ra \(\widehat {NOC’} = \widehat {NCM}\).
Do tứ giác \(NBMC\) nội tiếp nên \(\widehat {NBM} + \widehat {NCM} = {180^0}\).
Từ đó ta có \(\widehat {NOB’} + \widehat {NOC’} = {180^0}\). Vậy ba điểm \(O, B’, C’\) thẳng hàng hay \(B’C’\) là đường kính đường tròn \((C).\)
