Cho tam giác \(ABC\) có \(\widehat A = {60^0} , a = 10 , r = \dfrac{{5\sqrt 3 }}{3}\).
a) Tính \(R.\)
b) Tính \(b, c.\)
Giải
a) Ta có
\(2R = \dfrac{a}{{\sin A}} = \dfrac{{10}}{{\dfrac{{\sqrt 3 }}{2}}} = \dfrac{{20\sqrt 3 }}{3} \)
\( \Rightarrow R = \dfrac{{10\sqrt 3 }}{3}\).
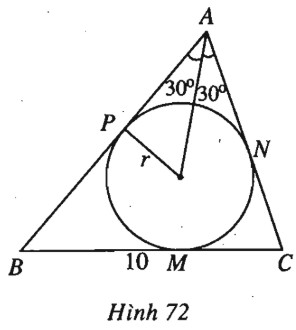
b) Gọi \(M, N, P\) lần lượt là các tiếp điểm của \(BC, CA, AB\) với đường tròn nội tiếp tam giác \(ABC\) (h.72).
Advertisements (Quảng cáo)
Ta có \(AP = AN = r.\cot {30^0} = 5 ; \)
\(BP + NC = BM + MC = a = 10\).
Từ đó ta có \((b - AN) + (c - AP) = 10\) hay \(b+c=20.\) (1)
Theo định lí cosin
\({a^2} = {b^2} + {c^2} - 2bc\cos {60^0}\) hay \({a^2} = {(b + c)^2} - 2bc - bc\), suy ra
\(bc = \dfrac{{{{(b + c)}^2} - {a^2}}}{3}\) \( = \dfrac{{{{20}^2} - {{10}^2}}}{3} = 100\) (2)
Từ (1) và (2) suy ra \(b, c\) là nghiệm của phương trình bậc hai \({x^2} - 20x + 100 = 0\).
Phương trình này có nghiệm kép \(b=c=10\) nên \(ABC\) là tam giác đều.
