Qua một điểm \(A\) cố định trên trục đối xứng của parabol \((P)\), ta vẽ một đường thẳng cắt \((P)\) tại hai điểm \(M\) và \(N\). Chứng minh rằng tích các khoảng cách từ \(M\) và \(N\) tới trục đối xứng của \((P)\) là hằng số.

(h.124).
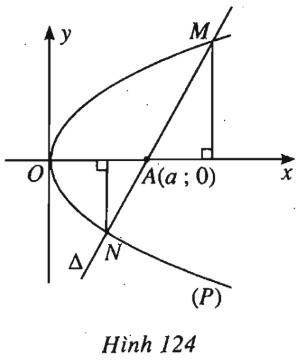
Chọn hệ trục tọa độ \(Oxy\) thích hợp sao cho parabol \((P)\) có phương trình : \({y^2} = 2px (p > 0)\) và \(A(a ; 0)\). Đường thẳng \(\Delta \) đi qua \(A\) có phương trình : \(\alpha (x - a) + \beta y = 0 ({\alpha ^2} + {\beta ^2} \ne 0)\).
Khi đó tung độ các giao điểm của đường thẳng \(\Delta \) và (P) là nghiệm của phương trình:
Advertisements (Quảng cáo)
\(\begin{array}{l}\alpha . \dfrac{{{y^2}}}{{2p}} + \beta y - \alpha a = 0\\ \Leftrightarrow \alpha {y^2} + 2p\beta y - 2p\alpha a = 0\,\,\,\,\,\,\,\,\,\,(1)\end{array}\)
Rõ ràng \(\alpha \ne 0\), vì nếu \(\alpha = 0\) thì đường thẳng \(\Delta \) trùng với trục hoành và chỉ cắt \((P)\) tại một điểm.
Do đó \(|{y_M}|.|{y_N}| = |{y_M}.{y_N}|\)
\(= \left| { - \dfrac{{2p\alpha a}}{\alpha }} \right| = 2p|a|\).
