Chứng minh rằng mỗi đường chuẩn của hypebol luôn đi qua chân các đường vuông góc kẻ từ tiêu điểm tương ứng tới hai đường tiệm cận.

(h.125).
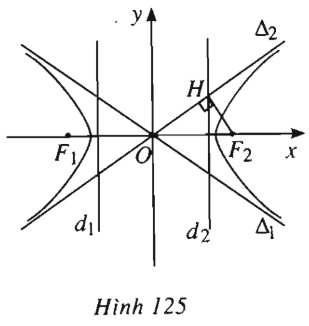
Xét hypebol \((H): \dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1\). \((H)\) có
Các tiêu điểm : \({F_1}( - c ; 0) , {F_2}(c ; 0)\).
Các đường chuẩn: \({d_1}: x = - \dfrac{a}{e} = - \dfrac{{{a^2}}}{c} , \) \( {d_2}: x = \dfrac{a}{e} = \dfrac{{{a^2}}}{c}\)
Advertisements (Quảng cáo)
Các tiệm cận :
\(\begin{array}{l}{\Delta _1}: y = - \dfrac{b}{a}x \Leftrightarrow \dfrac{x}{a} + \dfrac{y}{b} = 0\\{\Delta _2}: y = \dfrac{b}{a}x \Leftrightarrow \dfrac{x}{a} - \dfrac{y}{b} = 0.\end{array}\)
Gọi \(H = {d_2} \cap {\Delta _2}\). Suy ra tọa độ của \(H\) bằng \(\left( { \dfrac{{{a^2}}}{c} ; \dfrac{{ab}}{c}} \right)\).Do đó
\(\begin{array}{l}\overrightarrow {OH} = \left( { \dfrac{{{a^2}}}{c} ; \dfrac{{ab}}{c}} \right) ; \\ \overrightarrow {H{F_2}} = \left( {c - \dfrac{{{a^2}}}{c} ; - \dfrac{{ab}}{c}} \right).\\\overrightarrow {OH} .\overrightarrow {H{F_2}} \\ = \dfrac{{{a^2}}}{c}\left( {c - \dfrac{{{a^2}}}{c}} \right) + \dfrac{{ab}}{c}\left( { - \dfrac{{ab}}{c}} \right)\\= {a^2} - \dfrac{{{a^4}}}{{{c^2}}} - \dfrac{{{a^2}{b^2}}}{{{c^2}}}\\ = {a^2} - \dfrac{{{a^2}}}{{{c^2}}}\left( {{a^2} + {b^2}} \right) \\= {a^2} - \dfrac{{{a^2}}}{{{c^2}}}.{c^2} = 0\end{array}\)
Vậy \(OH \bot {F_2}H\). Do \((H)\) nhận \(Ox, Oy\) làm các trục đối xứng và \({\Delta _1} , {\Delta _2}\) cũng nhận \(Ox, Oy\) làm các trục đối xứng nên ta suy ra điều cần chứng minh.
