Bài 99 trang 121 SBT Hình học 10 Nâng cao. Gọi \(A’, B’\) thứ tự là hình chiếu của \(A, B\) trên đường chuẩn \(\Delta \) của \((P); F\) là tiêu điểm của \((P)\).. Bài 8. Ba đường cônic.
Cho \(A, B\) là hai điểm trên parabol \((P): {y^2} = 2px\) sao cho tổng các khoảng cách từ \(A\) và \(B\) tới đường chuẩn của \((P)\) bằng độ dài \(AB\). Chứng minh rằng \(AB\) luôn đi qua tiêu điểm của \((P).\)

(h.128).
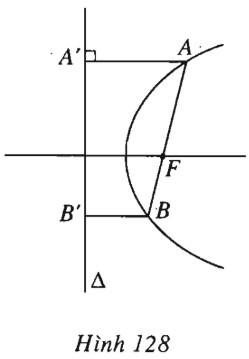
Gọi \(A’, B’\) thứ tự là hình chiếu của \(A, B\) trên đường chuẩn \(\Delta \) của \((P); F\) là tiêu điểm của \((P)\).
Ta có
Advertisements (Quảng cáo)
\(A, B \in (P) \Rightarrow AF = d(A ; \Delta ) = AA’ , \)
\(BF = d(B ; \Delta ) = BB’\).
Suy ra
\(AF+BF=AA’+BB’=AB.\)
Vậy \(A, B, F\) thẳng hàng hay \(AB\) đi qua \(F.\)
