Bài 98 trang 121 SBT Hình học 10 Nâng cao. \(AB = e(AA’ + BB’) > AA’ + BB’\). Bài 8. Ba đường cônic.
Cho hypebol \((P): \dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1\) và \(F(c ; 0)\) là một tiêu điểm của \((H)\). Một đường thẳng đi qua \(F\) và cắt \((H)\) tại hai điểm \(A, B\). Chứng minh rằng đường tròn đường kính \(AB\) cắt đường chuẩn : \(x = \dfrac{a}{e}\) của \((H).\)

(h.127).
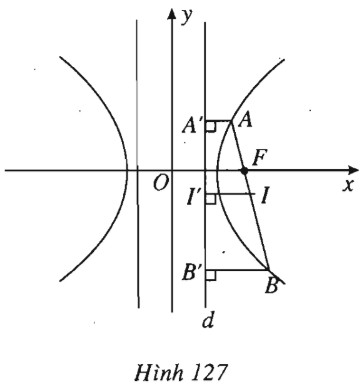
Làm tương tự như bài 97, ta cũng được:
Advertisements (Quảng cáo)
\(AB = e(AA’ + BB’) > AA’ + BB’\)
\(= 2II’\)
Vậy đường trò đường kính \(AB\) luôn cắt đường chuẩn \(d: x = \dfrac{a}{e}\).
