Giải các bất phương trình:
a) \(\dfrac{{1 - x}}{{\left( {2x - 1} \right)\left( {x - 2} \right)}} < 0\) ;
b) \(\dfrac{{x + 1}}{{2x + 1}} \ge \dfrac{{x - 1}}{{3x + 1}}\) .

a) Tập nghiệm \(S = \left( {\dfrac{1}{2};1} \right) \cup \left( {2; + \infty } \right).\)
b)
Advertisements (Quảng cáo)
\(\begin{array}{l}\dfrac{{x + 1}}{{2x + 1}} \ge \dfrac{{x - 1}}{{3x + 1}}\\ \Leftrightarrow \dfrac{{\left( {x + 1} \right)\left( {3x + 1} \right) - \left( {x - 1} \right)\left( {2x + 1} \right)}}{{\left( {2x + 1} \right)\left( {3x + 1} \right)}} \ge 0\\ \Leftrightarrow \dfrac{{{x^2} + 5x + 2}}{{\left( {2x + 1} \right)\left( {3x + 1} \right)}} \ge 0\\ \Leftrightarrow \dfrac{{\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)}}{{\left( {2x + 1} \right)\left( {3x + 1} \right)}} \ge 0.\end{array}\)
với \({x_1} = \dfrac{{ - 5 - \sqrt {17} }}{2}\) và \({x_2} = \dfrac{{ - 5 + \sqrt {17} }}{2}\). Ta lập bảng sau:
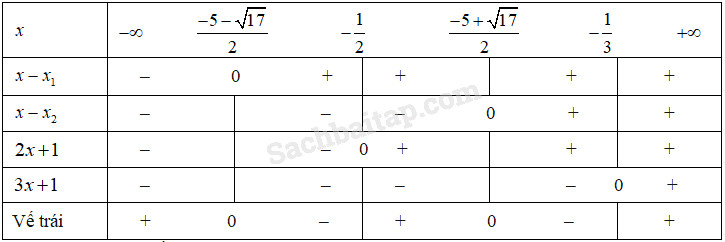
Vậy tập nghiệm của bất phương trình là
\(S = \left( { - \infty ,\dfrac{{ - 5 - \sqrt {17} }}{2}} \right) \cup \left( { - \dfrac{1}{2};\dfrac{{ - 5 + \sqrt {17} }}{2}} \right)\) \( \cup \left( { - \dfrac{1}{3}; + \infty } \right)\).
