Xét dấu của các biểu thức:
a. \(\dfrac{{x - 7}}{{4{{ {x}}^2} - 19{ {x + 12}}}}\)
b. \(\dfrac{{11{ {x}} + 3}}{{ - {x^2} + 5{ {x}} + 7}}\)
c. \(\dfrac{{3{ {x}} - 2}}{{{x^3} - 3{{ {x}}^2} + 2}}\)
d. \(\dfrac{{{x^2} + 4{ {x}} - 12}}{{\sqrt {6{{ {x}}^2}} + 3{ {x}} + \sqrt 2 }}\)
e. \(\dfrac{{{x^2} - 3{ {x}} - 2}}{{ - {x^2} + x - 1}}\)
f. \(\dfrac{{{x^3} - 5{ {x}} + 4}}{{{x^4} - 4{x^3} + 8{ {x}} - 5}}\)
 :
:
a. Đặt \(A\left( x \right) = \dfrac{{x - 7}}{{4{x^2} - 19x + 12}}.\) Tam thức \(4{x^2} - 19x + 12\) có hai nghiệm \({x_1} = \dfrac{3}{4},{x^2} = 4.\)
Lập bảng xét dấu \(A(x)\) :
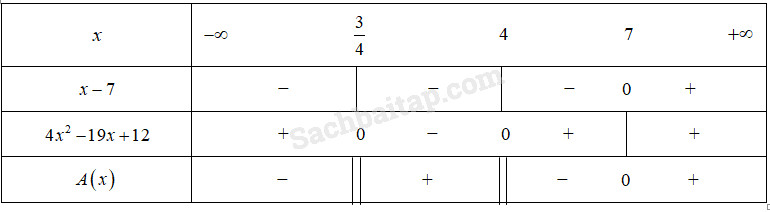
Từ bảng xét dấu ta thu được \(A(x) > 0\) trong các khoảng \(\left( {\dfrac{3}{4};4} \right)\) và \(\left( {7; + \infty } \right)\) và \(A(x) < 0\) trong các khoảng \(\left( { - \infty ;\dfrac{3}{4}} \right)\) và \(\,\left( {4;7} \right).\)
b. Đặt \(B\left( x \right) = \dfrac{{11x + 3}}{{ - {x^2} + 5x - 7}}.\) Tam thức \( - {x^2} + 5x - 7\) có a = -1 < 0 và biệt thức \(∆ = -3 < 0\) nên tam thức luôn luôn âm với mọi \(x\). Suy ra \(B(x) > 0\) \( \Leftrightarrow 11x + 3 < 0 \Leftrightarrow x < - \dfrac{3}{{11}}\) và \(B\left( x \right) < 0 \Leftrightarrow 11x + 3 > 0 \Leftrightarrow x > - \dfrac{3}{{11}}.\)
c. Đặt \(C\left( x \right) = \dfrac{{3x - 2}}{{{x^3} - 3{x^2} + 2}} = \dfrac{{3x - 2}}{{\left( {x - 1} \right)\left( {{x^2} - 2x - 2} \right)}}.\)
Lập bảng xét dấu (HS tự lập), ta thu được :
Advertisements (Quảng cáo)
\(C(x) > 0\) trong các khoảng \(\left( { - \infty ;1 - \sqrt 3 } \right),\left( {\dfrac{2}{3};1} \right)\) và \(\,\left( {1 + \sqrt 3 ; + \infty } \right).\)
\(C(x) < 0\) trong các khoảng \(\left( {1 - \sqrt 3 ;\dfrac{2}{3}} \right)\) và \(\,\left( {1;1 + \sqrt 3 } \right).\)
d. Đặt \(D\left( x \right) = \dfrac{{{x^2} + 4x - 12}}{{\sqrt 6 {x^2} + 3x + \sqrt 2 }}.\)
Ta thấy tam thức \(\sqrt 6 {x^2} + 3x + \sqrt 2 > 0\) với mọi \(x\), nên dấu của \(D(x)\) cùng dấu với dấu của tam thức \({x^2} + 4x - 12.\) Suy ra \(D(x) > 0\) trong các khoảng \(\left( { - \infty ; - 6} \right)\) và \(\,\left( {2; + \infty } \right),\) \(D(x) < 0\) trong khoảng \((-6 ; 2)\).
e. Đặt \(E\left( x \right) = \dfrac{{{x^2} - 3x - 2}}{{ - {x^2} + x - 1}}.\) Ta thấy \( - {x^2} + x - 1 < 0\) với mọi \(x\), nên \(E(x)\) trái dấu với dấu tam thức \({x^2} - 3x - 2.\)
Suy ra : \(E(x) > 0\) trong khoảng \(\left( {\dfrac{{3 - \sqrt {17} }}{2};\dfrac{{3 + \sqrt {17} }}{2}} \right).\)
\(E(x) < 0\) trong các khoảng \(\left( { - \infty ;\dfrac{{3 - \sqrt {17} }}{2}} \right)\) và \(\,\left( {\dfrac{{3 + \sqrt {17} }}{2}; + \infty } \right).\)
f. Đặt \(F\left( x \right) = \dfrac{{{x^3} - 5x + 4}}{{{x^4} - 4{x^3} + 8x - 5}}\)
\(= \dfrac{{\left( {x - 1} \right)\left( {{x^2} + x - 4} \right)}}{{{{\left( {x - 1} \right)}^2}\left( {{x^2} - 2x - 5} \right)}}.\)
Lập bảng xét dấu (Học sinh tự lập) ta thu được :
\(F(x) > 0\) trong các khoảng
\(\left( {\dfrac{{ - 1 - \sqrt {17} }}{2};1 - \sqrt 6 } \right),\left( {1;\dfrac{{ - 1 + \sqrt {17} }}{2}} \right)\) và \(\,\left( {1 + \sqrt 6 ; + \infty } \right).\)
\(F(x) < 0\) trong các khoảng
\(\left( { - \infty ;\dfrac{{ - 1 - \sqrt {17} }}{2}} \right),\) \(\left( {1 - \sqrt 6 ;1} \right),\) \(\left( {\dfrac{{ - 1 + \sqrt {17} }}{2};1 + \sqrt 6 } \right).\)
