Advertisements (Quảng cáo)
Cho hàm số \(f\left( x \right) = – x + \left| {x + 2} \right| – \left| {x – 2} \right|\).
a) Hãy viết hàm số dưới dạng hàm số bậc nhất trên từng khoảng và không chứa dấu giá trị tuyệt đối. (Gọi ý. Xét hàm số trên mỗi khoảng \(\left( { – \infty ; – 2} \right),\left[ { – 2;2} \right)\) và \(\left[ {2; + \infty } \right)\).
b) Chứng minh rằng \(y = f\left( x \right)\)là hàm số lẻ.
c) Vẽ đồ thị của hàm số \(y = f\left( x \right)\), lập bảng biến thiên và nêu sự biến thiên của nó trên mỗi khoảng kể trên.
d) Sử dụng đồ thị, hãy tìm các khoảng trên đó hàm số có giá trị dương.
a) \(f\left( x \right) = \left\{ \begin{array}{l} – x – 4\,\,khi\,\,x < – 2\\x\,\,\,\,\,\,\,\,\,\,\,\,\,khi – 2 \le x < 2\\ – x + 4\,\,khi\,\,x \ge 2.\end{array} \right.\)
b) Tập xác định của hàm số là R. Với mọi x, ta có:
Cách 1. (Sử dụng tính chất \(\left| { – a} \right| = \left| a \right|\)):
\(\begin{array}{l}f\left( { – x} \right) = – \left( { – x} \right) + \left| {\left( { – x} \right) + 2} \right| – \left| {\left( { – x} \right) – 2} \right|\\ = x + \left| {x – 2} \right| – \left| {x + 2} \right|\\ = – \left( { – x + \left| {x + 2} \right| – \left| {x – 2} \right|} \right)\\ = – f\left( x \right)\end{array}\)
Cách 2. (Sử dụng kết quả câu a):
Advertisements (Quảng cáo)
– Nếu \(x < – 2\) thì \( – x > 2\), nên \(f\left( { – x} \right) = – \left( { – x} \right) + 4 = – \left( { – x – 4} \right) = – f\left( x \right)\)
– Nếu \( – 2 \le x \le 2\)thì \( – 2 < – x \le 2\), nên \(f\left( { – x} \right) = – x = – f\left( x \right)\)
– Nếu \(x \ge 2\) thì \( – x \le – 2\), nên \(f\left( { – x} \right) = – \left( { – x} \right) – 4 = – \left( { – x + 4} \right) = – f\left( x \right)\).
Vậy trong mọi trường hợp ta đều có \(f\left( { – x} \right) = – f\left( x \right)\), chứng tỏ \(f\left( x \right)\) là số lẻ.
c) Đồ thị (h.1)
Bảng biến thiên
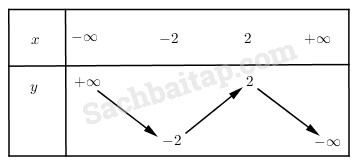
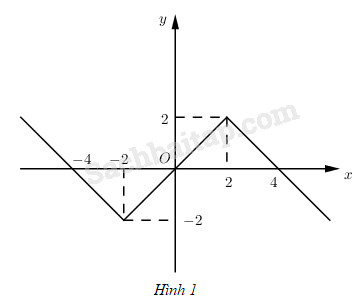
d) \(\left( { – \infty ; – 4} \right)\) và \(\left( {0;4} \right)\).