Một dây curoa quân quanh hai trục tròn tâm I bán kính 1dm và tâm J bán kính 5dm mà khoảng cách IJ là 8dm (h.6.1). Hãy tính độ dài của dây cu-roa.
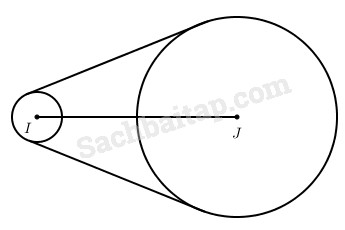

Gọi A, B là hai điểm tiếp xúc của dây curoa theo thứ tự với đường tròn tâm I và tâm J (A, B nằm cùng phía đối với đường thẳng IJ). Ta có \(\cos \widehat {BJI} = \dfrac{{R - r}}{d} = \dfrac{{5 - 1}}{8} = \dfrac{1}{2}\) (r = 1 là bán kính của đường tròn tâm I, R = 5dm là bán kính của đường tròn tâm J, \(d = IJ = 8dm\) là khoảng cách giữa hai tâm). Vậy \(\widehat {BJI} = \alpha = \dfrac{\pi }{3}\) .
Advertisements (Quảng cáo)
Dễ thấy chiều dai dây curoa bằng:
\(\begin{array}{l}2\left[ {R\left( {\pi - \alpha } \right) + r\alpha + d\sin \alpha } \right] = 2\left( {\dfrac{{11\pi }}{3} + 4\sqrt 3 } \right)\\ \approx 36,89\left( {dm} \right)\end{array}\)
