Chứng minh công thức \(\cos 2\alpha = 2{\cos ^2}\alpha - 1\)(với \(0 < \alpha < \dfrac{\pi }{4}\)) bằng “phương pháp hình học” như sau:
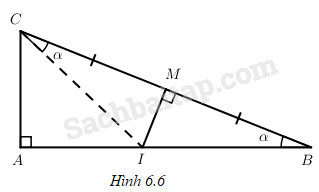
Xét tam giác vuông ABC với \(\widehat A = \dfrac{\pi }{2},\widehat B = \alpha .\) Kẻ đường trung trực của đoạn BC cắt AB tại I. Dễ thấy: \(\cos 2\alpha = \dfrac{{AI}}{{IC}};\cos \alpha = \dfrac{{AB}}{{BC}}\) (h. 6.6); từ đó hãy suy ra
\(\cos 2\alpha = 2{\cos ^2}\alpha - 1\).

Dễ thấy \(BI = IC,\)
Advertisements (Quảng cáo)
nên
\(\begin{array}{l}\cos 2\alpha = \dfrac{{AI}}{{IC}} = \dfrac{{AI}}{{BI}} = \dfrac{{AB - BI}}{{BI}}\\ = \dfrac{{AB}}{{BI}} - 1 = \dfrac{{AB}}{{BC}}.\dfrac{{2BM}}{{BI}} - 1\end{array}\)
Mà
\(\cos \alpha = \dfrac{{AB}}{{BC}} = \dfrac{{BM}}{{BI}}\), nên \(\cos 2\alpha = 2{\cos ^2}\alpha - 1\).
