Cho hàm số \(y = {x^2} - 4x + 1\)
a) Khảo sát và vẽ đồ thị (P) hàm số đã cho.
b) Gọi (d) là đường thẳng song song với đường phân giác của góc phần tư (I) và đi qua điểm M(0; m). Xác định biểu thức của hàm số có đồ thị (d).
c) Tìm hoành độ các giao điểm A và B (nếu có) của (d) và (P), và tọa độ trung điểm của đoạn thẳng AB (khi A và B phân biệt).

a) Hàm số \(y = {x^2} - 4x + 1\) nghịch biến trên khoảng \(\left( { - \infty ;2} \right)\); đồng biến trên khoảng \(\left( {2; + \infty } \right)\)
Đồ thị hàm số:
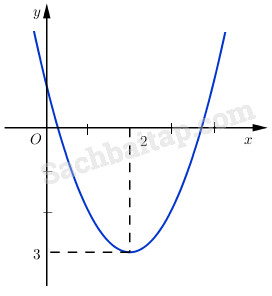
b) Hàm số cần tìm là \(y = x + m\) .
c) Hoành độ giao điểm của (d) và (P) là nghiệm của phương trình
Advertisements (Quảng cáo)
\({x^2} - 4x + 1 = x + m,\)
Hay \({x^2} - 5x + 1 - m = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
Phương trình (1) có biệt thức \(\Delta = 25 - 4\left( {1 - m} \right) = 21 + 4m\).
Do đó, nếu \(21 + 4m \ge 0\) thì nó có hai nghiệm
\({x_1} = \dfrac{{5 - \sqrt {21 + 4m} }}{2}\) và \({x_2} = \dfrac{{5 + \sqrt {21 + 4m} }}{2}\)
Đó cũng là hoành độ các giao điểm A và B của (d) và (P).
Tọa độ trung điểm của đoạn thẳng AB (khi \(\Delta = 21 + 4m > 0\)) là điểm có tọa độ \(\left( {{x_0};{y_0}} \right)\), trong đó:
\(\begin{array}{l}{x_0} = \dfrac{{{x_1} + {x_2}}}{2} = \dfrac{5}{2};\\{y_0} = {x_0} + m = \dfrac{5}{2} + m.\end{array}\)
