Lập bảng biến thiên và vẽ đồ thị của hàm số bậc hai
a) \(y = 2{x^2} + 4x - 6\)
b) \(y = - 3{x^2} - 6x + 4\)
c) \(y = \sqrt 3 {x^2} + 2\sqrt 3 x + 2\)
d) \(y = - 2({x^2} + 1)\)
Gợi ý làm bài
a) Hàm số bậc hai đã cho có a = 2; b = 4; c = -6;
Vậy \( - {b \over {2a}} = - 1;\Delta = {b^2} - 4ac = 64; - {\Delta \over {4a}} = - 8\)
Vì a > 0, ta có bảng biến thiên
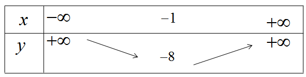
Hàm số nghịch biến trên khoảng \(( - \infty ; - 1)\) đồng biến trên khoảng \(( - 1; + \infty )\)
Để vẽ đồ thị ta có trục đối xứng là đường thẳng x = -1; đỉnh I(-1;-8); giao với tục tung tại điểm (0;-6); giao với trục hoành tại các điểm (-3;0) và (1;0).
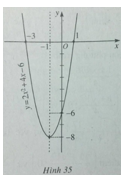
Đồ thị của hàm số \(y = 2{x^2} + 4x - 6\) được vẽ trên hình 35.
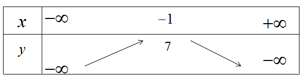
b) Bảng biến thiên
Advertisements (Quảng cáo)
Hàm số đồng biến trên khoảng \(( - \infty ; - 1)\) và nghịch biến trên khoảng \(( - 1; + \infty )\)
Đỉnh parabol I(-1;7). Đồ thị của hàm số \(y = - 3{x^2} - 6x + 4\) được vẽ trên hình 36.

c) Bảng biến thiên
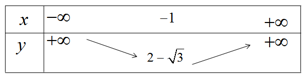
Hàm số nghịch biến trên khoảng \(( - \infty ; - 1)\) và đồng biến trên khoảng \(( - 1; + \infty )\)
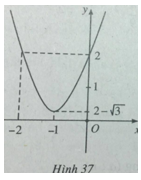
Đỉnh parabol \(( - 1;2 - \sqrt 3 )\)
Đồ thị hàm số được vẽ trên hình 37.
d) \(y = - 2{x^2} - 2\)
Bảng biến thiên
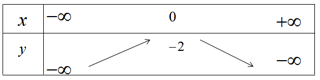
Hàm số đồng biến trên khoảng \(( - \infty ;0)\) và nghịch biến trên khoảng \((0; + \infty )\) , hàm số là chẵn.
Đỉnh parabol I(0;-2); đồ thị đi qua điểm (1;-4) và điểm (-1;-4).
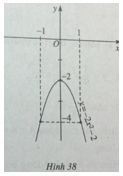
Đồ thị hàm số \(y = - 2({x^2} + 1)\) được vẽ trên hình 38.