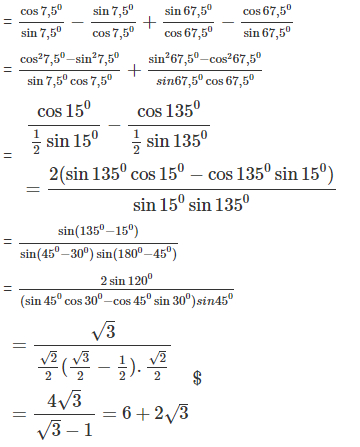Không sử dụng bảng số và máy tính, hãy tính. Bài 20 trang 194 Sách bài tập (SBT) Toán Đại số 10 - Bài 3: Công thức lượng giác
Không sử dụng bảng số và máy tính, hãy tính
a) \({\sin ^4}{\pi \over {16}} + {\sin ^4}{{3\pi } \over {16}} + {\sin ^4}{{5\pi } \over {16}} + {\sin ^4}{{7\pi } \over {16}}\)
b) \(\cot 7,{5^0} + \tan 67,{5^0} - \tan 7,{5^0} - \cot 67,{5^0}\)
Gợi ý làm bài
Advertisements (Quảng cáo)
a) \({\sin ^4}{\pi \over {16}} + {\sin ^4}{{3\pi } \over {16}} + {\sin ^4}{{5\pi } \over {16}} + {\sin ^4}{{7\pi } \over {16}}\)
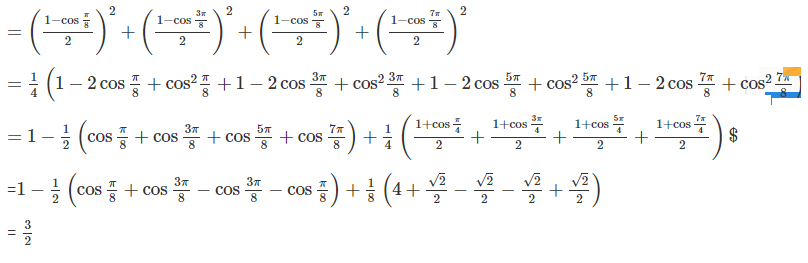
b) \(\cot 7,{5^0} + \tan 67,{5^0} - \tan 7,{5^0} - \cot 67,{5^0}\)