Trong mặt phẳng tọa độ Oxy cho đường tròn (C) : \({x^2} + {y^2} + 4x + 4y + 6 = 0\) và đường thẳng \(\Delta 😡 + my - 2m + 3 = 0\) với m là tham số thực.
a) Tìm tọa độ tâm I và bán kính R của đường tròn (C) ;
b) Tìm m để cắt (C) tại hai điểm phân biệt sao cho diện tích tam giác IAB đạt giá trị lớn nhất.
Gợi ý làm bài
(Xem hình 3.12)
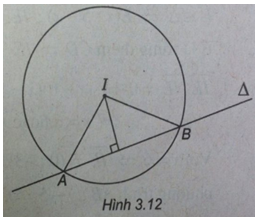
a) Đường tròn (C) có tâm I(-2;-2) và bán kính \(R = \sqrt {2.} \)
b) Diện tích tam giác IAB là :
\(S = {1 \over 2}IA.IB\sin AIB \le {1 \over 2}{R^2} = 1.\)
Advertisements (Quảng cáo)
S lớn nhất \( \Leftrightarrow S = 1\)
\( \Leftrightarrow \sin AIB = 1\)
\( \Leftrightarrow IA \bot IB\)
\( \Leftrightarrow d\left( {I,\Delta } \right) = {R \over {\sqrt 2 }}\)
\( \Leftrightarrow {{\left| { - 2 - 2m - 2m + 3} \right|} \over {\sqrt {1 + {m^2}} }} = 1\)
\( \Leftrightarrow {\left( {1 - 4m} \right)^2} = 1 + {m^2}\)
\( \Leftrightarrow 15{m^2} - 8m = 0\)
\( \Leftrightarrow m = 0$ hay $m = {8 \over {15}}\)
