Trong thiết bị ở Hình 2.13, bình hình trụ có bán kính r = 10 cm. Ta để một vật nhỏ áp vào thành trong của bình. Hệ số ma sát nghỉ giữa thành bình và vật là \({\mu _n} = 0,3\). Hỏi số vòng quay trong một phút của bình hình trụ phải như thế nào để vật bám được vào thành bình mà không bị rơi.

Phản lực \(\overrightarrow N \) của thành bình đặt lên vật là lực hướng tâm. Do có lực này mà xuất hiện lực ma sát nghỉ giữ cho vật khỏi bị rơi xuống (Hình 2.17G) :
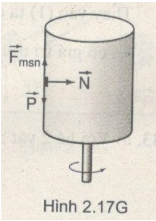
\({F_{msn}} = P\)
Advertisements (Quảng cáo)
Trong đó : P= mg
Và \({F_{msn}} \le {\mu _n}N = {\mu _n}m{\omega ^2}r = {\mu _n}m{(2\pi n)^2}r\)
Do đó : \(mg \le {\mu _n}m{(2\pi n)^2}r\)
Từ đó : \(n \ge {1 \over {2\pi }}\sqrt {{g \over {{\mu _n}r}}} \approx 2,88\) vòng/giây \( \approx 173\) vòng/phút.
