Một vật bắt đầu chuyển động trên một mặt dốc có hình dạng bất kì từ độ cao 1 m so với mặt nằm ngang (Hình 4.13). Tìm vận tốc của vật khi nó tới chân dốc. Bỏ qua má sát giữa vật và mặt dốc.
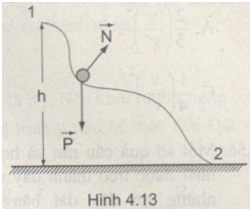

Vì chuyển động không có ma sát nên phản lực \(\overrightarrow N \) của mặt dốc tác dụng lên vật luôn vuông góc với phương độ dời và do đó không thực hiện công. Lực duy nhất thực hiện công là trọng lực \(\overrightarrow P \) nên ta có thể áp dụng định luật bảo toàn cơ năng để giải. Chọn mức không của thế năng tại mặt nằm ngang.
Tại vị trí xuát phát : Wđ = 0, \({W_{{t_1}}} = mgh\)
Tại chân dốc : \({{\rm{W}}_{{đ_2}}} = {{m{v^2}} \over 2},{{\rm{W}}_{{t_2}}} = 0\)
Theo định luật bảo toàn cơ năng :
Advertisements (Quảng cáo)
\({{\rm{W}}_{{đ_1}}} + {{\rm{W}}_{{t_1}}} = {{\rm{W}}_{{đ_2}}} + {{\rm{W}}_{{t_2}}}\)
Nên : \(\eqalign{ & mgh = {{m{v^2}} \over 2} \cr & v = \sqrt {2gh} = \sqrt {2.9,8.1} = 4,4m/s \cr} \)
Nhận xét : không thể giải bằng phương pháp động lực học vì
- không biết dạng cụ thể của quỹ đạo;
- thành phần lực theo phương chuyển dời luôn thay đổi theo từng vị trí.
