Advertisements (Quảng cáo)
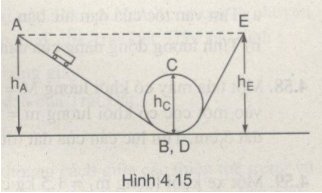
Một xe lăn có thể chuyển động trên một đường rãnh có dạng như Hình 4.15. Chiều cao hai đỉnh so với mặt đất là \({h_A} = {h_E} = 0,52m\) và chiều cao điểm C là \({h_C} = 0,30m.\) Xe được thả tự do từ A.
a) Bỏ qua ma sát. Hãy xác định các vận tốc tại các điểm B, C, D, E.
b) Xe có bị rời khỏi vòng tròn ở đỉnh C hay không ? Tại sao ? Sau khi xe tiếp tục chuyển động như thế nào ?
Lần lượt áp dụng định luật bảo toàn cơ năng cho từng vị trí.
\(\eqalign{ & a)mg{h_A} = {{mv_B^2} \over 2} \cr & {v_B} = \sqrt {2g{h_A}} = \sqrt {2.9,8.0,52} = 3,2m/s = {v_D} \cr & mg{h_A} = mg{h_C} + {{mv_C^2} \over 2} \cr & {v_C} = \sqrt {2g({h_A} – {h_C})} = \sqrt {2.9,8.0,22} = 2,1m/s \cr & mg{h_A} = mg{h_E} + {{mv_E^2} \over 2} \cr} \)
Vì \({h_A} = {h_E}\), nên suy ra \({v_E} = 0\).
b)Vận tốc của xe tại điểm C đủ để xe không rời quỹ đạo được xác định từ điều kiện :
\(mg = {{m{v^2}} \over r},\) hay \(v = \sqrt {gr} = \sqrt {g{{{h_C}} \over 2}} = \sqrt {9,8.0,15} = 1,2m/s.\)
Vậy, với vận tốc \({v_C} = 2,1m/s\), xe không bị rời khỏi quỹ đạo ở đỉnh C của vòng tròn. Sau khi tới E, xe dừng lại và chuyển động trở xuống, tiếp tục qua D, C,B rồi tới A nếu như má sát là không đáng kể.