Một bình hình trụ kín hai đầu , có độ cao là h , được đặt nằm ngang ,bên trong có một pít-tông có thể dịch chuyển không ma sát trong bình (Hình 6.2) .Lúc đầu pít-tông được giữ cố định ở chính giữa bình. Hai bên pít-tông đều có khí cùng loại áp suất khí bên trái lớn gấp n lần áp suất khí bên phải .Nếu bây giờ ta để pít-tông tự do thì pít-tông dịch chuyển như thế nào ? Nhiệt độ của hệ không đổi .
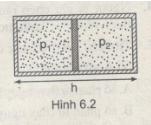

Khi để pít-tông tự do thì pít-tông dịch chuyển sang phải vì áp suất của khí bên trái lớn hơn .
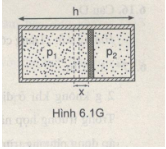
Gọi x là khoảng dịch chuyển của pít-tông (Hình 6.1G) và áp dụng định luật Bôi-lơ- Ma-ri-ốt cho mỗi lượng khí ở hai bên pít-tông , ta viết :
Advertisements (Quảng cáo)
\(\eqalign{ & {p_1}{h \over 2}S = p({h \over 2} + x)S(1) \cr & {p_2}{h \over 2}S = p({h \over 2} - x)S(2) \cr} \)
trong đó p1 và p2 là áp suất lúc đầu của khí bên trái và khí bên phải;p là áp suất cuối cùng của các khí, áp suất này giống nhau khi pít-tông đứng cân bằng .
Thay p1 = np2và giải hệ phương trình trên ta tìm được :\(x = \dfrac{{(n - 1)h}}{{2(n + 1)}}.\)