Bài 30. Cho tứ giác \(ABCD\). Gọi \(M, N\) lần lượt là trung điểm của \(AC\) và \(BD\). Chứng minh rằng \(A{B^2} + B{C^2} + C{D^2} + D{A^2} = A{C^2} + B{D^2} + 4M{N^2}\).

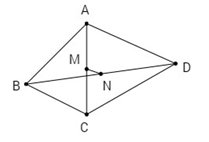
Áp dụng công thức tính trung tuyến, \(MN\) là trung tuyến của tam giác \(BMD\), ta có
\(M{N^2} = {{B{M^2} + D{M^2}} \over 2} - {{B{D^2}} \over 4}\,\,\,\,\, \Leftrightarrow \,\,4M{N^2} = 2(B{M^2} + D{M^2}) - B{D^2}\,\,\,(1)\)
Tương tự, \(BM, DM\) lần lượt là trung tuyến của tam giác \(ABC, ADC\) nên
Advertisements (Quảng cáo)
\(\eqalign{
& 4B{M^2} = 2(A{B^2} + B{C^2}) - A{C^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2) \cr
& 4D{M^2} = 2(D{A^2} + C{D^2}) - A{C^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(3) \cr} \)
Từ (2), (3) suy ra
\(2(B{M^2} + D{M^2}) = A{B^2}\, + B{C^2} + C{D^2} + D{A^2} - A{C^2}\,\,(4)\)
Thay (4) vào (1), ta có
\(\eqalign{
& \,\,\,\,\,\,\,\,4M{N^2} = A{B^2} + B{C^2} + C{D^2} + D{A^2} - A{C^2} - B{D^2} \cr
& \Rightarrow \,\,\,A{B^2} + B{C^2} + C{D^2} + D{A^2} = A{C^2} + B{D^2} + 4M{N^2} \cr} \)
