Cho tam giác \(ABC\) có độ dài ba trung tuyến bằng \(15, 18, 27.\)
a) Tính diện tích của tam giác.
b) Tính độ dài các cạnh của tam giác.
Giải
a) (h.68).
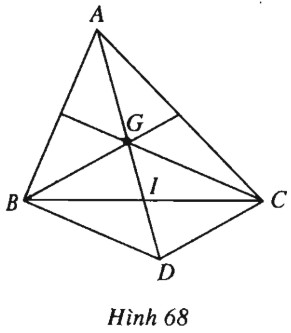
Gọi \(I\) là trung điểm của \(BC\) và \(G\) là trọng tâm của tam giác \(ABC\) thì
\(\dfrac{{{S_{ABC}}}}{{{S_{GBC}}}} = \dfrac{{AI}}{{GI}} = 3\)
Vậy \(S = 3{S_{GBC}}\).
Lấ điểm \(D\) là điểm đối xứng với \(G\) qua \(I\) ta được hình bình hành \(BGCD\), do đó
\({S_{GBC}} = {S_{BGD}} = \dfrac{1}{2}{S_{BGCD}}\).
Advertisements (Quảng cáo)
Vậy \({S_{ABC}} = 3{S_{BGD}}\).
Tam giác \(BGD\) có độ dài ba cạnh bằng \(10, 12, 18\) nên
\({S_{BGD}}\) \(= \sqrt {20.(20 - 10)(20 - 12)(20 - 18)} \)\( = \sqrt {20.10.8.2} = 40\sqrt 2 \).
Vậy \(S = 3.40\sqrt 2 = 120\sqrt 2 \).
b) Giả sử \({m_a} = 15, {m_b} = 18 , {m_c} = 27\). Ta có
\(\left\{ \begin{array}{l}{b^2} + {c^2} = 2{m_a}^2 + \dfrac{{{a^2}}}{2}\\{c^2} + {a^2} = 2m_b^2 + \dfrac{{{b^2}}}{2}\\{a^2} + {b^2} = 2m_c^2 + \dfrac{{{c^2}}}{2}\end{array} \right. \\ \Rightarrow {a^2} + {b^2} + {c^2} \\= \dfrac{4}{3}.\left( {m_a^2 + m_b^2 + m_c^2} \right) = 1704.\)
Ta lại có
\(\begin{array}{l}{b^2} - {a^2} = \dfrac{4}{3}\left( {m_a^2 - m_b^2} \right) = - 132 ; \\{b^2} - {c^2} = \dfrac{4}{3}\left( {m_c^2 - m_b^2} \right) = 540.\end{array}\)
Từ đó ta tính được \(b = 8\sqrt {11} ; a = 2\sqrt {209} ; c = 2\sqrt {41} .\)
