Bài 80 trang 50 SBT Hình học 10 Nâng cao. Trên ngọn đồi có một cái tháp cao \(100m\) (h.24). Đỉnh tháp \(B\) và chân tháp \(C\) nhìn điểm \(A\) ở chân đồi dưới các góc. Bài 3. Hệ thức lượng trong tam giác.
Trên ngọn đồi có một cái tháp cao \(100m\) (h.24). Đỉnh tháp \(B\) và chân tháp \(C\) nhìn điểm \(A\) ở chân đồi dưới các góc tương ứng bằng \(30^0\) và \(60^0\) so với phương thẳng đứng. Xác định chiều cao \(HA\) của ngọn đồi.
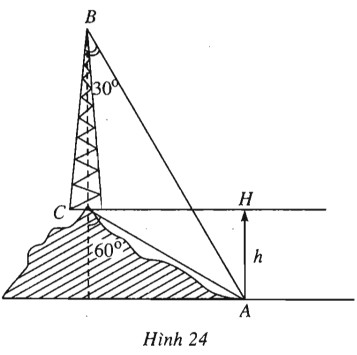
Giải
\(\widehat {ABC} = {30^{0\,}}\,;\,\widehat {ACB} = {120^0}\)
\(\Rightarrow \,\,\widehat A = {30^0}\).
Advertisements (Quảng cáo)
Từ đó suy ra \(AC=CB=100 \)
\( \Rightarrow AH = AC.\sin \widehat {ACH} = 50\).
Chiều cao của ngọn đồi là \(50\) mét.
