Dựa vào đồ thị, hãy cho biết tập hợp các giá trị của x sao cho y ≥ 0. Bài 31 trang 59 SGK Đại số 10 nâng cao - Bài 3: Hàm số bậc hai
Hàm số \(y{\rm{ }} = {\rm{ }} - 2{x^2} - {\rm{ }}4x{\rm{ }} + {\rm{ }}6\) có đồ thị là Parabol (P).
a) Tìm tọa độ đỉnh, phương trình trục đối xứng của (P).
b) Vẽ Parabol (P).
c) Dựa vào đồ thị, hãy cho biết tập hợp các giá trị của x sao cho y ≥ 0
a) Ta có: a = -2; b = -4; c = 6
\(\eqalign{
& {x_0} = {{ - b} \over {2a}} = {4 \over { - 4}} = - 1 \cr
& \Rightarrow {y_0} = - 2{( - 1)^2} - 4( - 1) + 6 = 8 \cr} \)
Tọa độ đỉnh (P) là: \(I = (-1; 8)\)
Advertisements (Quảng cáo)
Phương trình trục đối xứng của (P) là: \(x = -1\)
b)
Đồ thị (P):
Giao đồ thị với \(Ox\) :
\(y = 0 \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
x = - 3 \hfill \cr} \right.\)
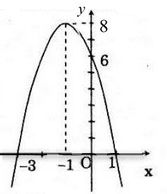
c) Ta có:
\(y ≥ 0 ⇔ -3 ≤ x ≤ 1\)