Chứng minh rằng diện tích của một tứ giác bằng nửa tích hai đường chéo và sin của góc hợp bởi hai đường chéo đó.. Bài 32 trang 66 SGK Hình học 10 nâng cao - Bài 3. Hệ thức lượng trong tam giác
Bài 32. Chứng minh rằng diện tích của một tứ giác bằng nửa tích hai đường chéo và sin của góc hợp bởi hai đường chéo đó.
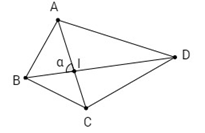
Gọi \(I\) là giao điểm của hai đường chéo \(AC, BD\) và \(\widehat {AIB} = \alpha \).
Ta có \({S_{ABI}} = {1 \over 2}AI.BI.\sin \alpha \,\,\,\,\,{S_{ADI}} = {1 \over 2}AI.DI.\sin ({180^0} - \alpha ) = \,{1 \over 2}AI.DI.\sin \alpha \,\)
Advertisements (Quảng cáo)
Suy ra \({S_{ABD}} = {S_{ABI}} + {S_{ADI}} = {1 \over 2}AI.(BI + DI).\sin \alpha = {1 \over 2}AI.BD.\sin \alpha \)
Tương tự ta suy ra \({S_{BCD}} = {S_{BIC}} + {S_{CDI}} = {1 \over 2}CI.BD.\sin \alpha \)
Từ đó suy ra
\({S_{ABCD}} = {S_{ABD}} + {S_{BCD}} = {1 \over 2}.BD.(AI + CI).\sin \alpha = {1 \over 2}.BD.AC.\sin \alpha. \)