Phân tích các đa thức sau thành nhân tử bậc nhất rồi xét dấu:. Bài 33 trang 126 SGK Đại số 10 nâng cao - Bài 4: Dấu của nhị thức bậc nhất
Phân tích các đa thức sau thành nhân tử bậc nhất rồi xét dấu:
a) \(–x^2+ x + 6\)
b) \(2{x^2} - (2 + \sqrt 3 )x + \sqrt 3 \)

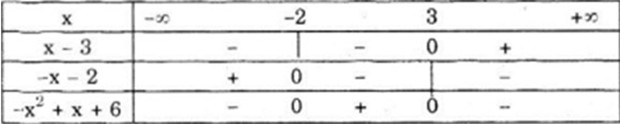
a) Phương trình \(–x^2+ x + 6 = 0\) có hai nghiệm : x1 = -2 và x2 = 3
Nên \(–x^2 + x + 6= -(x + 2)(x – 3) = (-x-2)(x-3)\)
Ta có bảng xét dấu:
Advertisements (Quảng cáo)
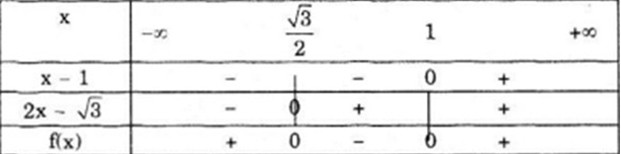
b) Phương trình \(2{x^2} - (2 + \sqrt 3 )x + \sqrt 3 \) = 0 có hai nghiệm là x1 = 1 và \({x_2} = {{\sqrt 3 } \over 2}\)
Do đó:
\(2{x^2} - (2 + \sqrt 3 )x + \sqrt 3 = 2(x - 1)(x - {{\sqrt 3 } \over 2}) \)
\(= (x - 1)(2x - \sqrt 3 )\)
Ta có bảng xét dấu sau: