Giải các bất phương trình
a) \({{(3 - x)(x - 2)} \over {x + 1}} \le 0\)
b) \({3 \over {1 - x}} \ge {5 \over {2x + 1}}\)
c) \(|2x - \sqrt 2 |\, + \,|\sqrt 2 - x|\, > \,3x - 2\)
d) \(|(\sqrt 2 - \sqrt 3 )x + 1|\, \le \,\sqrt 3 + \sqrt 2 \)
Đáp án
a) Ta có bảng xét dấu:
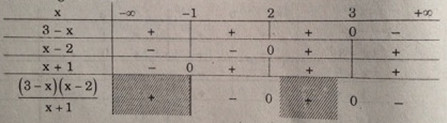
Vậy tập nghiệm của bất phương trình \({{(3 - x)(x - 2)} \over {x + 1}} \le 0\) là:
\(S = (-1, 2] ∪ [3, +∞)\)
b) Ta có:
\({3 \over {1 - x}} \ge {5 \over {2x + 1}} \Leftrightarrow {{3(2x + 1) - 5(1 - x)} \over {(1 - x)(2x + 1)}} \ge 0 \Leftrightarrow {{11x - 2} \over {(1 - x)(2x + 1)}} \ge 0\)
Bảng xét dấu:
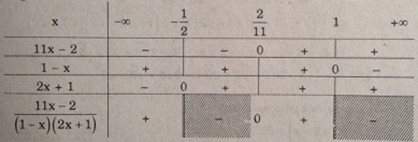
Tập nghiệm của bất phương trình đã cho là: \(S = ( - \infty ; - {1 \over 2}) \cup {\rm{[}}{2 \over {11}},1)\)
c) Ta có bảng xét dấu:
Advertisements (Quảng cáo)

i) Với \(x < {{\sqrt 2 } \over 2}\) , ta có:
\(\eqalign{
& (1) \Leftrightarrow - 2x + \sqrt 2 + \sqrt 2 - x > 3x - 2 \cr&\Leftrightarrow 6x < 2\sqrt 2 + 2 \cr
& \Leftrightarrow x < {{\sqrt 2 + 1} \over 3} \cr} \)
Vì \({{\sqrt 2 } \over 2} < {{\sqrt 2 + 1} \over 3} \Rightarrow x < {{\sqrt 2 } \over 2}\)
ii) Với \({{\sqrt 2 } \over 2} \le x < \sqrt2\) , ta có:
\((1) \Leftrightarrow 2x - \sqrt 2 + \sqrt 2 - x > 3x - 2 \Leftrightarrow x < 1\)
Kết hợp điều kiện ta có: \({{\sqrt 2 } \over 2} \le x < 1\)
iii) Với \(x \ge \sqrt 2 \)
\((1) \Leftrightarrow 2x - \sqrt 2 - \sqrt 2 + x > 3x - 2\)
\(\Leftrightarrow - 2\sqrt 2 > - 2\) (vô nghiệm)
Vậy tập nghiệm của bất phương trình là: \(S = ( - \infty ,{{\sqrt 2 } \over 2}) \cup {\rm{[}}{{\sqrt 2 } \over 2},1) = ( - \infty ,1)\)
d) Áp dụng: \(|A| ≤ B ⇔ -B ≤ A ≤ B\)
Ta có:
\(\eqalign{
& |(\sqrt 2 - \sqrt 3 )x + 1|\, \le \,\sqrt 3 + \sqrt 2 \cr
& \Leftrightarrow - \sqrt 3 - \sqrt 2 \le (\sqrt 2 - \sqrt 3 )x + 1 \le \sqrt 3 + \sqrt 2 \cr
& \Leftrightarrow - \sqrt 3 - \sqrt 2 - 1 \le (\sqrt 2 - \sqrt 3 )x \le \sqrt 3 + \sqrt 2 - 1 \cr
& \Leftrightarrow {{ - \sqrt 3 - \sqrt 2 - 1} \over {\sqrt 2 - \sqrt 3 }} \ge x \ge {{\sqrt 3 + \sqrt 2 - 1} \over {\sqrt 2 - \sqrt 3 }} \cr
& \Leftrightarrow (\sqrt 3 + \sqrt 2 + 1)(\sqrt 3 + \sqrt 2 ) \ge x \ge \cr&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(1 - \sqrt 3 - \sqrt 2 )(\sqrt 3 + \sqrt 2 ) \cr
& \Leftrightarrow 5 + 2\sqrt 6 + \sqrt 3 + \sqrt 2 \ge x \ge \cr&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;- 5 - 2\sqrt 6 + \sqrt 3 + \sqrt 2 \cr} \)
Vậy \(S = {\rm{[}} - 5 - 2\sqrt 6 + \sqrt 3 + \sqrt 2 ;\,5 + 2\sqrt 6 + \sqrt 3 + \sqrt 2 )\)
