Giải các hệ bất phương trình
a)
\(\left\{ \matrix{
(x - 3)(\sqrt 2 - x) > 0 \hfill \cr
{{4x - 3} \over 2} < x + 3 \hfill \cr} \right.\)
b)
\(\left\{ \matrix{
{2 \over {2x - 1}} \le {1 \over {3 - x}} \hfill \cr
|x| < 1 \hfill \cr} \right.\)
Đáp án
a) Ta có bảng xét dấu:
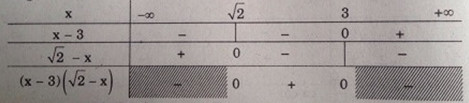
Ta có:
\(\eqalign{
& (x - 3)(\sqrt 2 - x) > 0 \Leftrightarrow \sqrt 2 < x < 3\,\,(1) \cr
& {{4x - 3} \over 2} < x + 3 \Leftrightarrow 2x < 9 \Leftrightarrow x < {9 \over 2}\,\,\,(2) \cr} \)
Từ (1) và (2) ta có: \(\sqrt 2 < x < 3\)
Advertisements (Quảng cáo)
Vậy \(S = (\sqrt 2 ,3)\)
b) Ta có:
\(\eqalign{
& {2 \over {2x - 1}} \le {1 \over {3 - x}} \Leftrightarrow {2 \over {2x - 1}} - {1 \over {3 - x}} \le 0 \cr
& \Leftrightarrow {{6 - 2x - 2x + 1} \over {(2x - 1)(3 - x)}} \le 0 \Leftrightarrow {{ - 4x + 7} \over {(2x - 1)(3 - x)}} \le 0 \cr} \)
Bảng xét dấu:
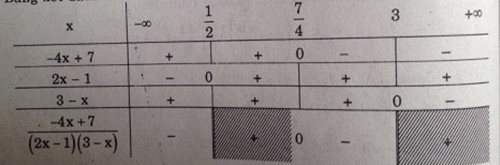
Ta có:
\({{ - 4x + 7} \over {(2x - 1)(3 - x)}} \le 0 \Leftrightarrow \left[ \matrix{
x < {1 \over 2} \hfill \cr
{7 \over 4} \le x < 3 \hfill \cr} \right.\)
Hệ đã cho tương đương với:
\(\left\{ \matrix{
\left[ \matrix{
x < {1 \over 2} \hfill \cr
{7 \over 4} \le x < 3 \hfill \cr} \right. \hfill \cr
- 1 < x < 1 \hfill \cr} \right. \Leftrightarrow - 1 < x < {1 \over 2}\)
Vậy \(S = ( - 1;{1 \over 2})\)
