Chứng minh rằng:. Bài 38 trang 109 SGK Hình học 10 Nâng cao - Bài 6. Đường hypebol
Cho đường tròn (C) tâm \({F_1}\) , bán kính R và một điểm \({F_2}\) ở ngoài (C). Chứng minh rằng tập hợp tâm các đường tròn đi qua \({F_2}\) , tiếp xúc với (C) là một đường hypebol. Viết phương trình chính tắc của hypebol đó.
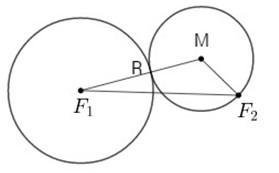
Gọi M là tâm đường tròn đi qua \({F_2}\) và tiếp xúc với (C)
Ta có: \(|M{F_1} - M{F_2}| = R = 2a\)
Advertisements (Quảng cáo)
Vậy tập hợp các điểm M là đường hypebol (H) có \(a = {R \over 2},c = {{{F_1}{F_2}} \over 2}\)
\( \Rightarrow {b^2} = {c^2} - {a^2} = {{{F_1}{F_2}^2 - {R^2}} \over 4}\)
Phương trình chính tắc của (H) là:
\({{{x^2}} \over {{{\left( {{R \over 2}} \right)}^2}}} - {{{y^2}} \over {{{\left( {{{\sqrt {{F_1}{F_2}^2 - {R^2}} } \over 2}} \right)}^2}}} = 1.\)