Advertisements (Quảng cáo)
Giải và biện luận các bất phương trình
a) \((2x – \sqrt 2 )(x – m) > 0\)
b) \({{\sqrt 3 – x} \over {x – 2m + 1}} \le 0\)
Ta có:
\(\eqalign{
& (2x – \sqrt 2 ) = 0 \Leftrightarrow x = {{\sqrt 2 } \over 2} \cr
& x – m = 0 \Leftrightarrow x = m \cr} \)
i) Với \(x < {{\sqrt 2 } \over 2}\) , ta có bảng xét dấu:
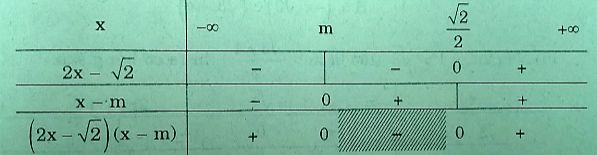
Vậy \(S = ( – \infty ;m) \cup ({{\sqrt 2 } \over 2}, + \infty )\)
ii) Với \(m = {{\sqrt 2 } \over 2}\) thì bất phương trình trở thành:
\(\eqalign{
& (2x – \sqrt 2 )(x – {{\sqrt 2 } \over 2}) > 0 \Leftrightarrow {(2x – \sqrt 2 )^2} > 0 \cr
& \Leftrightarrow x \ne {{\sqrt 2 } \over 2} \cr
& S = R\backslash {\rm{\{ }}{{\sqrt 2 } \over 2}{\rm{\} }} \cr} \)
iii) Với \(m > {{\sqrt 2 } \over 2}\) , ta có bảng xét dấu:
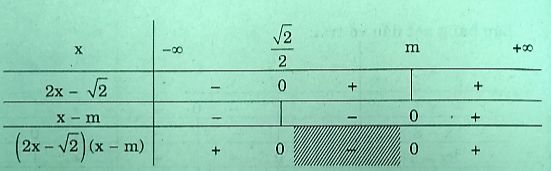
\(S = ( – \infty ;{{\sqrt 2 } \over 2}) \cup (m; + \infty )\)
b) Ta có:
\(\eqalign{
& \sqrt 3 – x = 0 \Leftrightarrow x = \sqrt 3 \cr
& x – 2m + 1 = 0 \Leftrightarrow x = 2m – 1 \cr} \)
i) Nếu \(2m – 1 < \sqrt 3 \Leftrightarrow m < {{\sqrt 3 + 1} \over 2}\) , ta có bảng sau:
\(S = \left( { – \infty ;2m – 1} \right) \cup \left[ {\sqrt 3 ; + \infty } \right)\)
ii) Nếu \(2m – 1 = \sqrt 3 \Leftrightarrow m = {{\sqrt 3 + 1} \over 2}\) thì dễ thấy tập nghiệm là:
\(S = ( – \infty ,\sqrt 3 ) \cup (\sqrt 3 , + \infty )\)
iii) Nếu \(2m – 1 > \sqrt 3 \Leftrightarrow m > {{\sqrt 3 + 1} \over 2}\) thì ta có bảng sau:
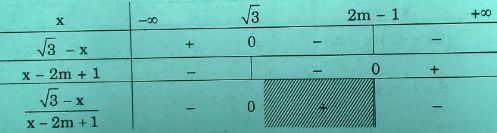
Vậy tập nghiệm là \(S = ( – \infty ,\sqrt 3 ) \cup (2m – 1; + \infty )\)