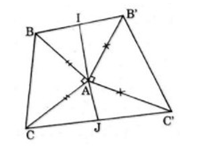
Trên hình 63 có vẽ hai tam giác vuông cân ABC và A’B’C’ có chung đỉnh A. Gọi I và J lần lượt là trung điểm của hai đoạn thẳng BB’ và CC’. Chứng minh rằng
a) \(AI \bot C{C’}\,\,AJ \bot B{B’}\,\);
b) \(B{C’}\,\, \bot {B’}C\,\,\).

Ta có \(\overrightarrow {AI} = {1 \over 2}(\overrightarrow {AB} + \overrightarrow {A{B’}} )\,\,;\,\,\overrightarrow {AJ} = {1 \over 2}(\overrightarrow {AC} + \overrightarrow {A{C’}} )\)
\(\eqalign{
& \Rightarrow \,\,\overrightarrow {AI} .\,\overrightarrow {C{C’}} = {1 \over 2}(\overrightarrow {AB} + \overrightarrow {A{B’}} ).\,(\overrightarrow {A{C’}} - \overrightarrow {AC} ) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {1 \over 2}(\overrightarrow {AB} .\,\overrightarrow {A{C’}} - \overrightarrow {AB} .\overrightarrow {AC} + \overrightarrow {A{B’}} .\,\overrightarrow {A{C’}} - \overrightarrow {A{B’}} .\,\overrightarrow {AC} ) \cr} \)
Vì \(AB \bot AC\,\,\,A{B’} \bot A{C’}\,\) nên \(\overrightarrow {AB} .\,\overrightarrow {AC} = \overrightarrow {A{B’}} .\,\overrightarrow {A{C’}} = 0\)
Mặt khác
\(\eqalign{
& \overrightarrow {AB} .\,\overrightarrow {A{C’}} = AB.\,A{C’}.\cos \widehat {BA{C’}} \cr
& \overrightarrow {A{B’}} .\,\overrightarrow {AC} = A{B’}.\,AC.\cos \widehat {{B’}AC} \cr
& \Rightarrow \,\,\,\overrightarrow {AB} .\,\overrightarrow {A{C’}} = \overrightarrow {A{B’}} .\,\overrightarrow {AC} \,\, \Rightarrow \,\,\overrightarrow {AI} .\,\overrightarrow {C{C’}} = 0\,\, \Rightarrow \,\,AI \bot C{C’} \cr} \)
Advertisements (Quảng cáo)
Tương tự \(\overrightarrow {AJ} .\,\overrightarrow {B{B’}} = {1 \over 2}(\overrightarrow {AC} + \overrightarrow {A{C’}} ).\,(\overrightarrow {A{B’}} - \overrightarrow {AB} )\)
\(\eqalign{
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {1 \over 2}(\overrightarrow {AC} .\,\overrightarrow {A{B’}} - \overrightarrow {AC} .\overrightarrow {AB} + \overrightarrow {A{C’}} .\,\overrightarrow {A{B’}} - \overrightarrow {A{C’}} .\,\overrightarrow {AB} ) =0\cr
& \Rightarrow \,\,AJ \bot B{B’} \cr} \)
b) Ta có
\(\eqalign{
& \overrightarrow {B{C’}} .\,\overrightarrow {{B’}C} = (\overrightarrow {A{C’}} - \overrightarrow {AB} ).\,(\overrightarrow {AC} - \overrightarrow {A{B’}} ) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \overrightarrow {A{C’}} .\,\overrightarrow {AC} - \overrightarrow {A{C’}} .\,\overrightarrow {A{B’}} - \overrightarrow {AB} .\,\overrightarrow {AC} + \overrightarrow {AB} .\,\overrightarrow {A{B’}} \cr} \)
\(\overrightarrow {AB} .\,\overrightarrow {A{B’}} = AB.A{B’}.\cos \widehat {BA{B’}}\)
\(\overrightarrow {AC} .\,\overrightarrow {A{C’}} = AC.A{C’}.\cos ({180^0} - \widehat {BA{B’}}) \)
\(= - \overrightarrow {AB} .\,\overrightarrow {A{B’}}.\)
Do đó: \(\overrightarrow {B{C’}} .\,\overrightarrow {{B’}C} =\overrightarrow 0\)
Vậy \(B{C’} \bot {B’}C\).
