Cho hình vuông ABCD cạnh a. Gọi N là trung điểm của CD, M là điểm trên AC sao cho \(AM = {1 \over 4}AC.\)
a)Tính các cạnh của tam giác BMN.
b) Có nhận xét gì về tam giác BMN ? Tính diện tích tam giác đó.
c) Gọi I là giao điểm của BN và AC. Tính CI.
d) Tính bán kính đường tròn ngoại tiếp tam giác BDN.

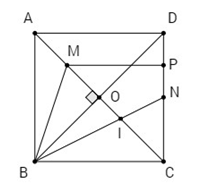
a) Gọi O là tâm của hình bình hành ABCD thì M là trung điểm AO.
\(\eqalign{
& B{N^2} = B{C^2} + N{C^2} \cr
& \,\,\,\,\,\,\,\,\,\,\, = {a^2} + {{{a^2}} \over 4} = {{5{a^2}} \over 4}\,\, \Rightarrow \,\,BN = {{a\sqrt 5 } \over 2} \cr
& B{M^2} = B{O^2} + O{M^2} \cr
& \,\,\,\,\,\,\,\,\,\,\,\, = {\left( {{{a\sqrt 2 } \over 2}} \right)^2} + {\left( {{{a\sqrt 2 } \over 4}} \right)^2} = {{5{a^2}} \over 8} \cr
& \,\,\,\, \Rightarrow \,\,BM = {{a\sqrt {10} } \over 4} \cr} \)
Kẻ MP // AD ta có
Advertisements (Quảng cáo)
\(M{N^2} = M{P^2} + P{N^2} = {\left( {{{3a} \over 4}} \right)^2} + {\left( {{a \over 4}} \right)^2} = {{10{a^2}} \over {16}}\,\,\)
\(\Rightarrow \,\,MN = {{a\sqrt {10} } \over 4}\)
b) Ta có
\(MB = MN\,\,\,B{N^2} = M{B^2} + M{N^2}\) nên tam giác BMN vuông cân tại M. Diện tích tam giác BMN là
\({S_{BMN}} = {1 \over 2}M{N^2} = {1 \over 2}.{{10{a^2}} \over {16}} = {{5{a^2}} \over {16}}\)
c) Ta có I là trọng tâm tam giác BCD nên \(IC = {2 \over 3}IO = {2 \over 3}.a.{{\sqrt 2 } \over 2} = {{a\sqrt 2 } \over 3}\).
d) Gọi R là bán kính đường tròn ngoại tiếp tam giác BDN.
Áp dụng định lí sin ta có
\({{BN} \over {\sin \widehat {BDN}}} = 2R\,\, \Rightarrow \,\,R = \,{{BN} \over {2\sin {{45}^0}}} = {{a\sqrt 5 } \over 2}.{1 \over {\sqrt 2 }} = {{a\sqrt {10} } \over 4}\)
