Giải bất phương trình và bất phương trình
a) |x + 1| + |x – 1| = 4
b) \({{|2x - 1|} \over {(x + 1)(x - 2)}} > {1 \over 2}\)

a) Ta có bảng xét dấu:
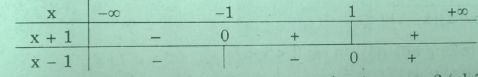
i) Với \(x < -1\), ta có (1) \(⇔ - x – 1 – x + 1 = 4 ⇔ x = -2\) (nhận)
ii) Với \(-1 ≤ x ≤ 1\), ta có: (1) \(⇔ x + 1 – x + 1 = 4 ⇔ 2 = 4\) (vô nghiệm)
iii) Với \(x > 1\), ta có (1) \(⇔ x + 1 + x – 1 = 4 ⇔ x = 2\) (nhận)
Vậy S = {-2, 2}
b) Ta có:
i) Nếu \(x \le {1 \over 2}\) thì bất phương trình trở thành: \({{ - 2x + 1} \over {(x + 1)(x - 2)}} > {1 \over 2}\)
Advertisements (Quảng cáo)
Ta có:
\(\eqalign{
& {{ - 2x + 1} \over {(x + 1)(x - 2)}} > {1 \over 2}\cr& \Leftrightarrow {{2( - 2x + 1) - (x + 1)(x - 2)} \over {2(x + 1)(x - 2)}} > 0 \cr
& \Leftrightarrow {{ - {x^2} - 3x + 4} \over {2(x + 1)(x - 2)}} > 0 \Leftrightarrow {{(x - 1)(x + 4)} \over {2(x + 1)(x - 2)}} < 0 \cr} \)
Lập bảng xét dấu:
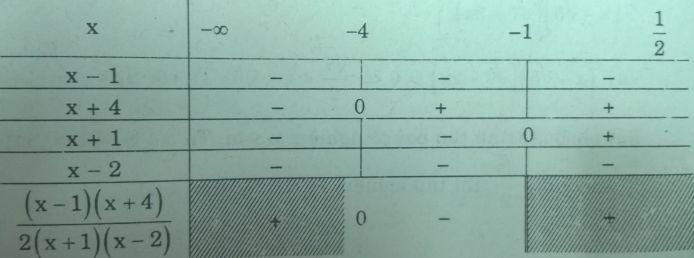
Trường hợp này ta có: \(-4 < x < -1\)
ii) Nếu \(x > {1 \over 2}\) thì bất phương trình đã cho trở thành: \({{2x - 1} \over {(x + 1)(x - 2)}} > {1 \over 2}\)
Ta có:
\(\eqalign{
& {{2x - 1} \over {(x + 1)(x - 2)}} > {1 \over 2} \cr&\Leftrightarrow {{2(2x - 1) - (x + 1)(x - 2)} \over {2(x + 1)(x - 2)}} > 0 \cr
& \Leftrightarrow {{x(x - 5)} \over {2(x + 1)(x - 2)}} < 0 \cr} \)
Lập bảng xét dấu trên nửa khoảng \(({1 \over 2}, + \infty )\)
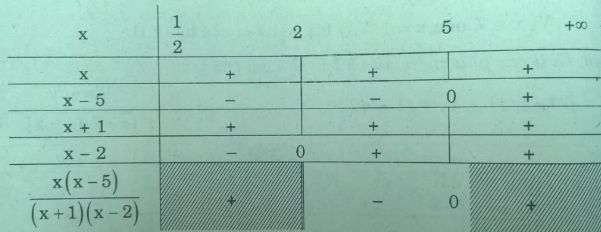
Trong trường hợp này ta có: \(2 < x < 5\)
Vậy \(S = (-4, -1) ∪ (2, 5)\)
